計算ミスがなくならない5つの原因

今回は数学や、計算を伴う理科の問題に関するお話です。

 

ケアレスミスの中でも代表的なのが計算ミス。その原因についてまずはお話ししましょう。

 

 

こちらは連立方程式の問題です。

小数や分数も混ざっており、正答率はあまり高くないでしょう。

 

この問題を解こうと、ある生徒が下のような計算式を書いたとします（架空の答案です）。

みなさんは、これを見てどう感じるでしょうか？

 

 

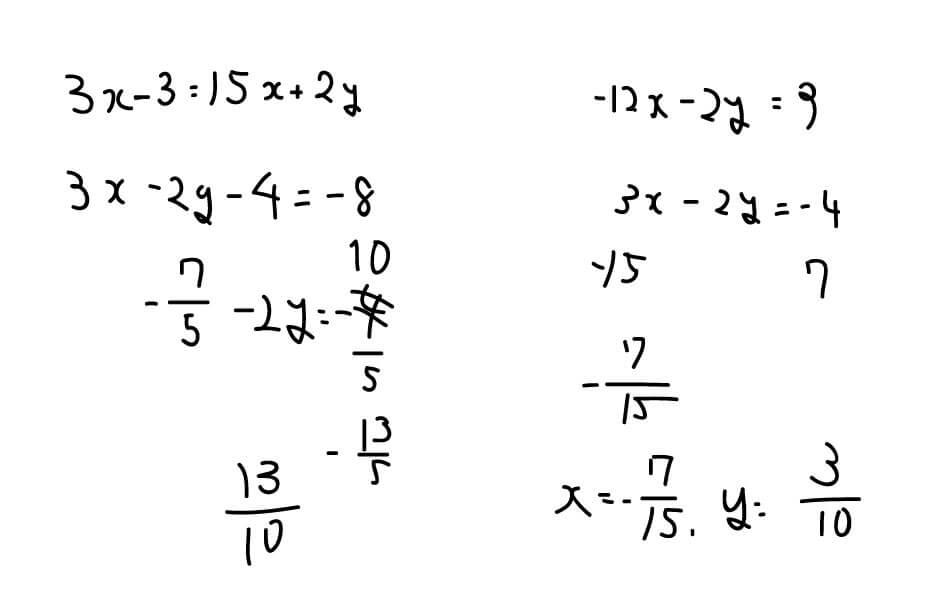
ここで出されている答えは、不正解です。

 

はっきり言って、このような答案の書き方からは、計算ミスを防ごうという気持ちが感じられません。

むしろ、自分からミスをしにいっているようにすら見えます。

 

ここには、計算ミスがなくならない5つの悪いクセが含まれているからです。

 

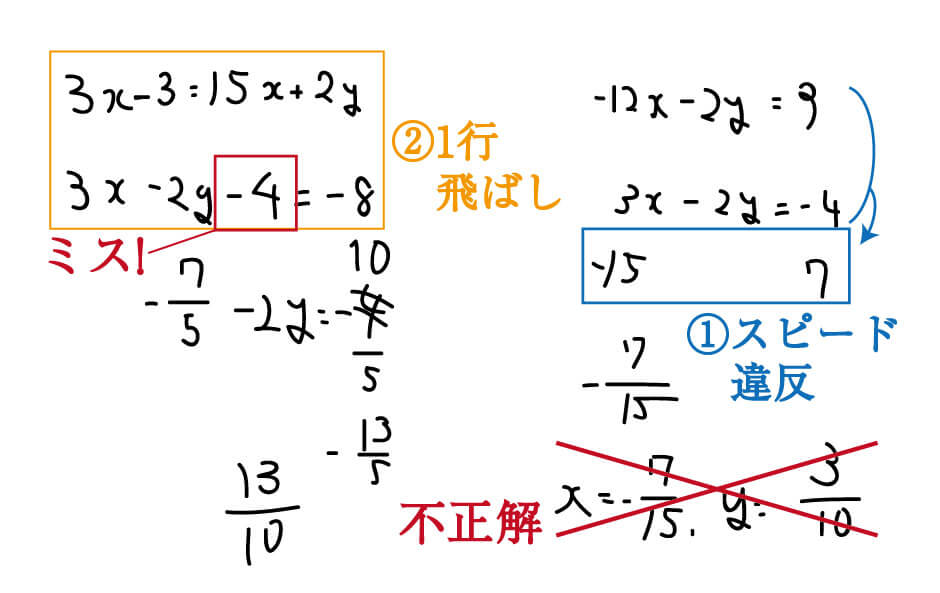
① スピード違反

 

上の答案例の青い枠で囲まれた部分を見てください。

ここでは、\(-12x-2y＝3\)と\(3x-2y＝4\)という2つの方程式から、加減法によって\(-2y\)を消し、\(x\)の値を出そうとしています。

ところが、本来は\(-15x＝7\)と書くべき途中の計算式を、“\(x＝\)”を省略し、「\(-15　7\)」と書いています。

解答時間が限られていて焦っている中では、こういった省略をして、とにかくスピード重視で計算しがちです。

 

そうして速く解くことばかりに気を取られていると、自分の計算能力を超えたスピードになってしまい、頭の処理が追いつかずミスが起きやすくなります。

もちろん、ものすごくゆっくり計算すればOKというわけではありません。

そうではなく、“スピード違反”は禁物ということです。

 

② 1行飛ばし

 

計算ミスの原因の中で、最もよくやってしまいがちなのが‟1行飛ばし”です。

 

答案例のオレンジ色の線で囲われた部分を見てください。

 

\begin{eqnarray}
\left\{
\begin{array}{l}
0.3（x-1）＝1.5x＋0.2y　【1】 & \\
\cfrac{x}{2} – \cfrac{y-2}{3} = – \cfrac{4}{3} 　【2】&
\end{array}
\right.
\end{eqnarray}

⇓

\begin{eqnarray}
\left\{
\begin{array}{l}
3x-3＝15x＋2y 　【1】& \\
3x-2y-4＝-8　【2】 &
\end{array}
\right.
\end{eqnarray}

 

どちらの方程式も、両辺に同じ数字を掛けて小数または分数を整数にする計算と、分配法則による計算をいっぺんに行っています。

この処理によって、ある1つのミスを引き起こしてしまいました。

 

正しく計算すると【2】の式は\(3x-2y＋4＝-8\)となるはずですが、両辺に\(6\)を掛けた後、\(-2（y-2）\)を展開する際、\(4\)につける符号を間違ってしまったのです。

 

なぜこのようなミスが起きたかというと、1行飛ばしをしたからです。

計算というのは、1つの行で複数の作業をするとミスしやすくなります。

逆に言えば、下記のように1つの行につき1つの作業に留めておけば、計算ミスは減るということです。

 

\(\cfrac{x}{2} – \cfrac{y-2}{3} = – \cfrac{4}{3} \)
\(3x-2（y-2）＝-8 \)　←両辺に\(6\)を掛ける
\(3x-2y＋4＝-8\)　←分配法則

 

③ 途中計算が単なるラクガキ

 

今回例に挙げた答案は多少大げさなものですが、このように何の計算がどこに書かれているのかパッと見てわからない、きつい言い方をすれば“ラクガキ”のような答案になってしまう生徒は少なくありません。

 

これでは、ミスなく答えを出すのは難しいでしょう。

 

④ 字が小さい&読み取れない

 

\(6\)を\(0\)と読みまちがえたり、\(7\)を\(1\)と見まちがえたりしてしまった。あるいは、繰り上がりの\(1\)という数字を小さ過ぎて見落としてしまった。

 

誰もが経験のあるミスではないでしょうか。

③にも通じることですが、焦って答案を作り、自分で書いたのに解読できないような文字や数字で計算していては、なかなか計算ミスは減りません。

 

⑤ まちがいやすいポイントを知らない

 

今回の例題でいえば、【2】の式の\(-\cfrac{y-2}{3}\)がミスの起きやすいポイント。マイナスがついた分数式は、誤った符号をつけてしまいがちだからです。

 

このようなまちがいやすいポイントを意識できていないことも、ミスが減らない大きな理由と言えます。

「1行につき1作業」で計算ミスを防ごう

ここからは、計算ミスを引き起こす一番の要因である‟1行飛ばし”について掘り下げていきたいと思います。

突然ですが、みなさんは次のような経験をしたおぼえはないでしょうか?

 

 

こういったうっかりミスは、普段よくあることだと思います。

 

元々「飲み物を取りにいく」という明確な目的があったのに、結局何も持たずに部屋へ戻ってしまった。

これは、ただ単に忘れてしまったわけではありません。

途中で母親から別の情報が与えられ、「飲み物を取りに行く」という記憶が上書きされてしまったのです。

 

これと同じようなことが、計算ミスをする過程で頻繁に起こっています。

 

その具体例を挙げていきましょう。

 

 

こちらは帯分数の割り算です。

このような問題を解こうとするとき、みなさんは次の流れで計算していくと思います。

 

①割り算をするために帯分数を仮分数に直す

②割り算を掛け算に変えて、割る分数の分母と分子をひっくり返す（逆数にする）

 

上記の例では、これら2つの作業をいっぺんに行ったところ、ミスが起こってしまいました。

仮分数に直し、割り算を掛け算に直すところまではできていますが、逆数に変える作業を忘れてしまったのです。

 

①と②の作業が必要なことは知っていたのに、両方をいっぺんに行ったことで、「逆数にする」という情報が他の情報に上書きされてしまった。

 

では、どうすれば計算ミスを防げたかというと、①と②をわけて作業すればよかったのです。

 

\(2\cfrac{1}{4}÷1\cfrac{1}{5}\)

\(＝\cfrac{9}{4} ÷\cfrac{6}{5}\)　←①帯分数を仮分数に直す

\(＝\cfrac{9}{4} ×\cfrac{5}{6}\)　←②逆数を掛ける

 

このように、1行につき1つの動作を徹底すれば、計算ミスはグッと減るでしょう。

 

みなさんはテストになるとできる限り速く問題を解こうと、途中の計算を省略してしまいがちです。それがミスにつながります。

1行飛ばしはケガのもとと肝に銘じておきましょう。

 

 

こちらも1行飛ばしによってミスをしてしまった典型的な例。

通分と分配法則をいっぺんに行ったため、\(4b\)につける符号をまちがえてしまいました。

 

やはりこの場合も、「1行につき１つの作業」というルールを守っていれば、ミスを防ぐことができるのです。

 

\(\cfrac{3a＋5b}{2}-\cfrac{a-2b}{3}\)

\(=\cfrac{3(3a＋5b)-2(a-2b)}{6}\) 　←通分

\(=\cfrac{9a＋15b-2a＋4b}{6}\) 　←分配法則

 

このように計算式を省かずに書いていくことを「面倒くさい」と感じる人がいるかもしれませんが、それではいけません。

その面倒くささがミスのもとだからです。

 

そういった面倒だという感覚は捨てて、練習でも本番でも計算式をていねいに書いていく習慣をつけましょう。

 

 

関連記事 ⇒ ケアレスミスが多い方必見!　万全の対策法を解説

 

関連記事 ⇒ ミスの記録 と 正しいテストの見直し方法