【数学】三角錐の体積比を楽に求められる公式 ～受験の秒殺テク（2）～

2020.09.14

中学生向け

高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる“秒殺テクニック”を紹介していきます。

今回は、三角すいの“ちぢみ率”を求める問題を取り上げます（ちぢみ率というのは、本講義だけで使用する言い方です）。

例題を見てみましょう。

これが、ちぢみ率を求める問題。三角すい全体に対して、灰色の部分の小さな三角すいがどれくらい縮まっているのか、ということです。

これをきちんと計算しようとすると、三角すいOABCの底面を△OAB、三角すいODEFの底面を△ODEと考えて△OABと△ODEの比率を求め、CとFから底面までの距離（高さ）を比べ──という風に、とても時間がかかってしまいます。

ここで役立つのが、今回の秒殺テクニックです。

三角すいの内部で、一方向へ縮んだ三角すいの体積は、以下の公式で求めることができます。

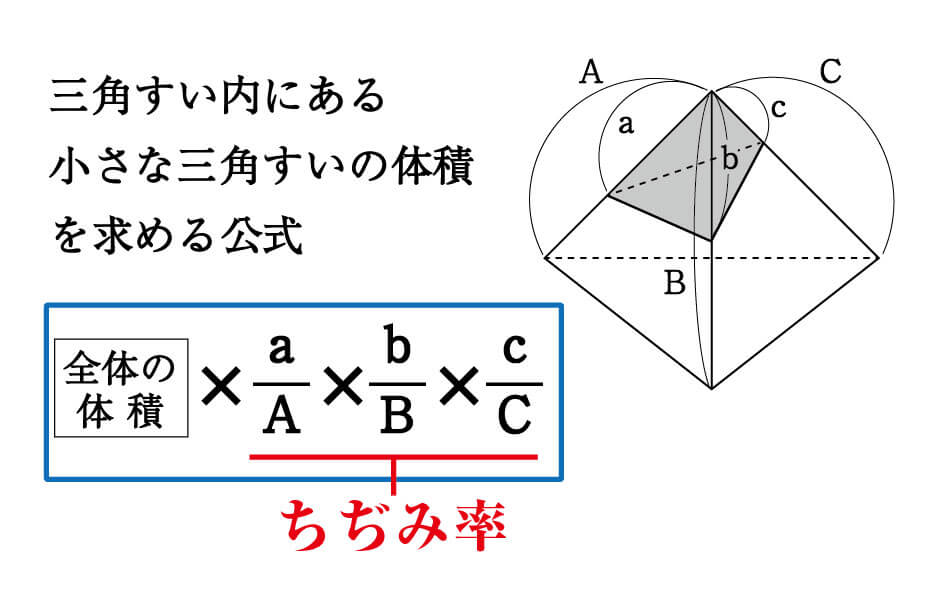
全体の体積に、\(\frac{a}{A}\)、\(\frac{b}{B}\)、\(\frac{c}{C}\)をかけたものが、小さい三角すいの体積です。

この\(\frac{a}{A}\)、\(\frac{b}{B}\)、\(\frac{c}{C}\)をかけ合わせた分数が、本講義で“ちぢみ率”と呼んでいるもの。

ちぢみ率は、元の三角すいに対してどれくらい縮小したのかを表す分数なので、そのまま例題の答えになります。

実際に解いてみましょう。

各辺の比は、次のように表すことができます。

AO：DO＝3：2

BO：EO＝2：1

CO：FO＝4：1

よって、全体に対する三角すいODEFのちぢみ率は、以下となります。

\begin{eqnarray}
\cfrac{2}{3}×\cfrac{1}{2}×\cfrac{1}{4} = \cfrac{1}{12}倍
\end{eqnarray}

それでは、類題で練習してみてください。

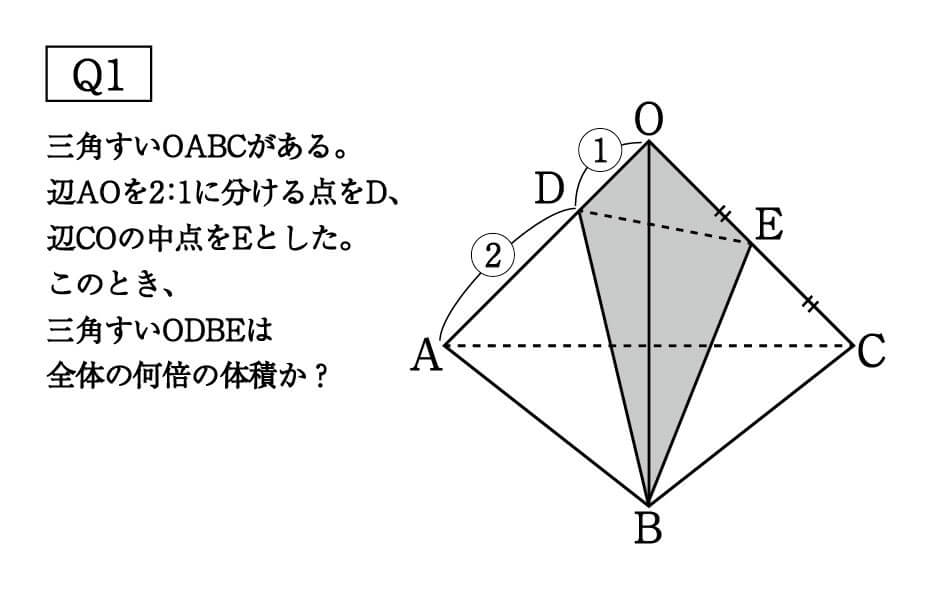
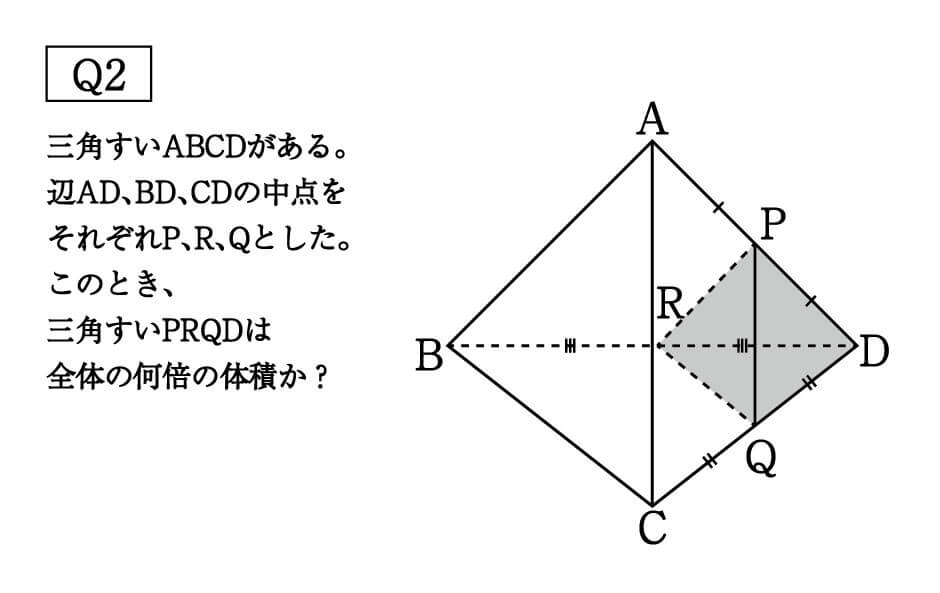
以下が答えになります。

Q1：\(\cfrac{1}{3}×\cfrac{1}{1}×\cfrac{1}{2}＝\cfrac{1}{6}\)倍

Q2：\(\cfrac{1}{2}×\cfrac{1}{2}×\cfrac{1}{2}＝\cfrac{1}{8}\)倍

Q2は縮んでいく方向が、右下の頂点Dであることに気をつけましょう。