正三角形の問題を速攻で解くための2大公式

高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる“秒殺テクニック”を紹介していきます。

 

今回のテーマは正三角形の2大公式です。

これらの公式をおぼえれば、正三角形の高さと面積を瞬間的に出すことができます。

 

 

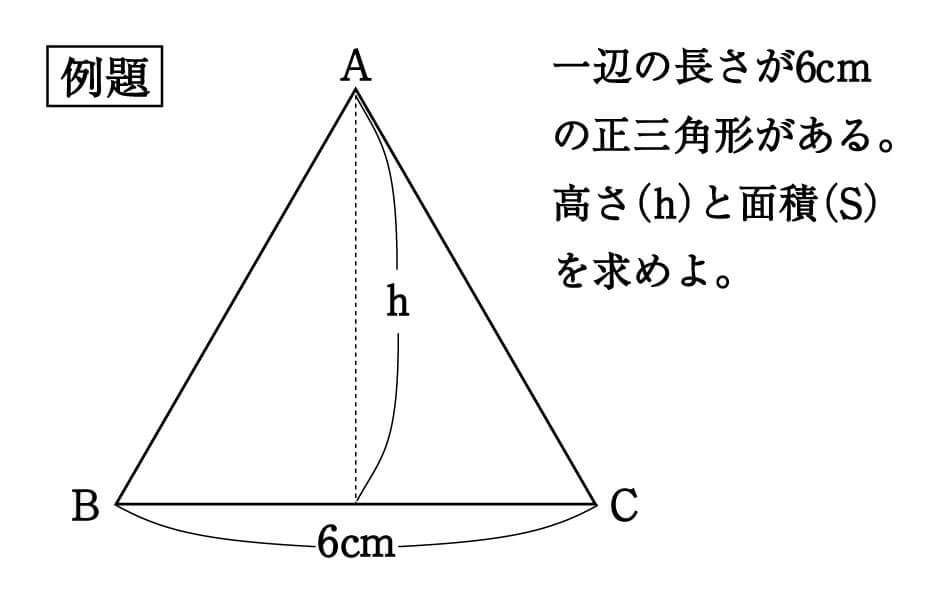
まずはこちらの例題を、一般的なやり方で解いてみましょう。

 

正三角形の高さにあたる線を引き、底辺との交点をOとします。

二等辺三角形の性質により、高さにあたる垂線は底辺を二等分するので、直角三角形ABOの底辺は3cmです。

 

 

∠ABOは、正三角形のひとつの角なので60°、よって∠BAOは30°。

つまり△ABOは、30°、60°、90°という3つの角で構成された直角三角形であることがわかります。

 

この直角三角形は、三辺の比が\(1：2：\sqrt{3}\) になる特別な図形です。そのため、高さは\(3\sqrt{3}cm\) 。

 

面積は当然、底辺×高さ×\(\frac{1}{2}\)で求められるので、以下の通りです。

 

 

こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。

 

その公式がこちらです。

 

 

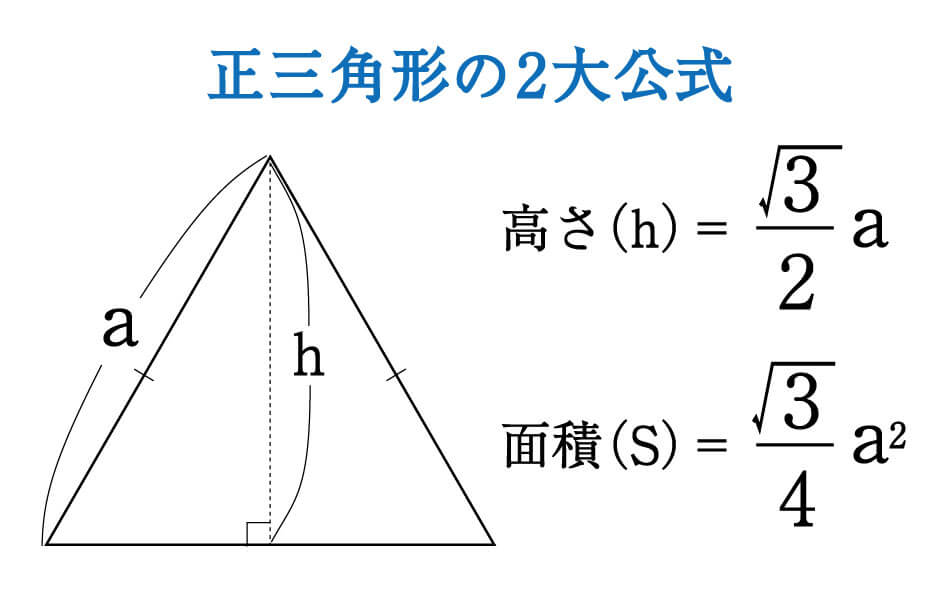
aに正三角形の一辺の長さを代入すれば、わずかなで時間で高さと面積を求めることが可能になります。

ただ、この公式のやっかいなところは「おぼえにくい」ということ。

 

そこで、この数式のまま暗記するのではなく、おぼえ方を変えてみましょう。

 

① 一辺を半分にする

② (半分)\(\sqrt{3}\) ⇒ 高さ（h）

③ (半分)\(^2\sqrt{3}\) ⇒ 面積（S）

 

正三角形が出てきたら、一辺の長さを半分にします。それに\(\sqrt{3}\) をつければ高さ、二乗して\(\sqrt{3}\) をつければ面積。

これだけです。

 

この方法で、例題を解いてみましょう。

 

 

① 一辺を半分にする ⇒ \(3cm\)

② (半分)\(\sqrt{3}\) ⇒ \(3\sqrt{3}cm\)

③ (半分)\(^2\sqrt{3}\) ⇒ \(9\sqrt{3}cm^2\)

 

こうすれば、5秒以内に答えが出せますよね。

 

「なぜ、これで正解が出せるの？」と疑問に思うかもしれませんが、何のことはありません。ただ公式の順番を入れかえただけなんです。

 

 

それでは、類題を使ってトレーニングしてみましょう。

Q1～Q3の高さと面積を求めてください。

 

 

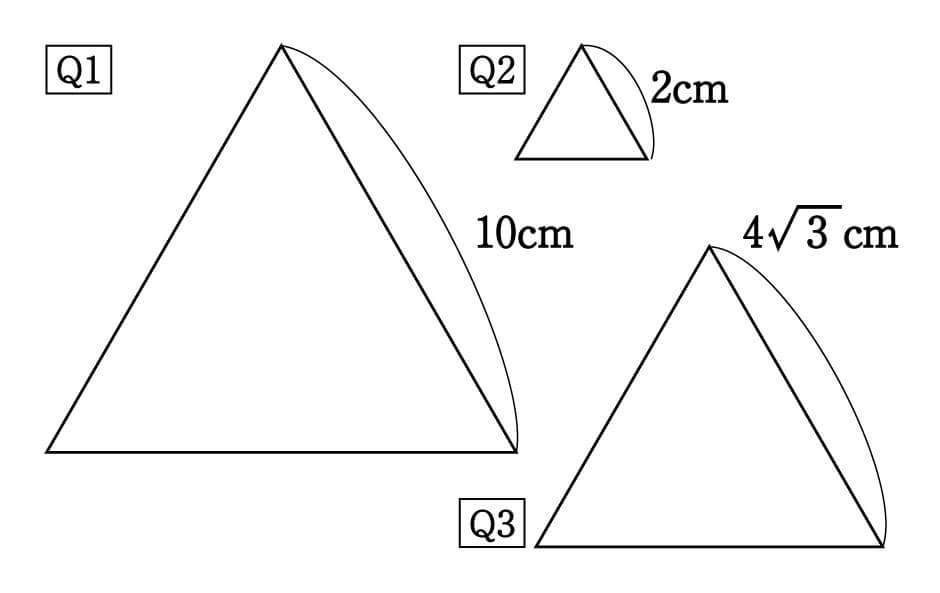
答えはこちらです。

 

Q3はやや難しいので、落ち着いて計算するようにしましょう。

 

また、以下のように正六角形の面積を聞かれる問題もあります。

 

 

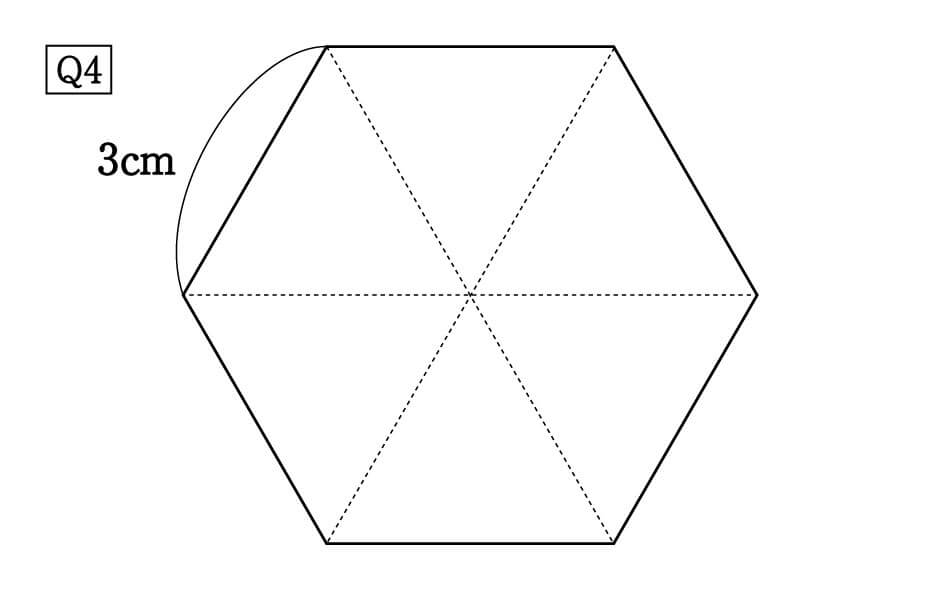
正六角形というのは、同じ正三角形が6つ集まってできたものです。

そのため、ひとつの正三角形の面積を求めて、6倍すれば答えが求められます。

 

 

前回の記事 ⇒ メネラウスの定理：覚え方のコツ!
次の記事 ⇒ 三平方の定理が成り立つ三辺の比：最重要7パターン