切頭円柱と切頭四角柱の体積を求める公式

今回は切断された立体（切頭〇〇柱）の体積を求めるテクニックを紹介していきます。

 

 

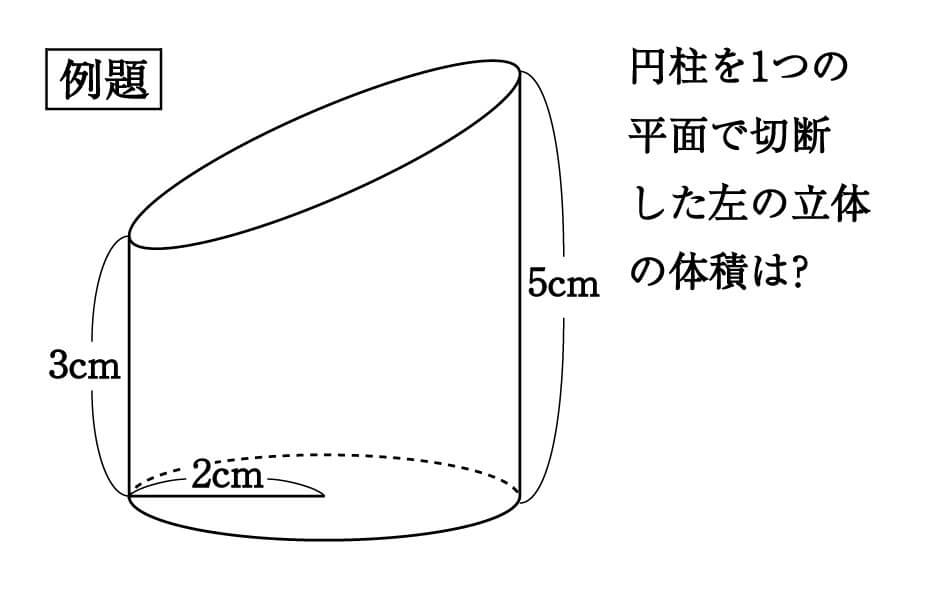
こちらの例題では、斜めに切断された円柱の体積が問われています。

このような立体を切頭円柱と呼んだりします。

 

まずは、一般的な考え方で解いてみましょう。

 

 

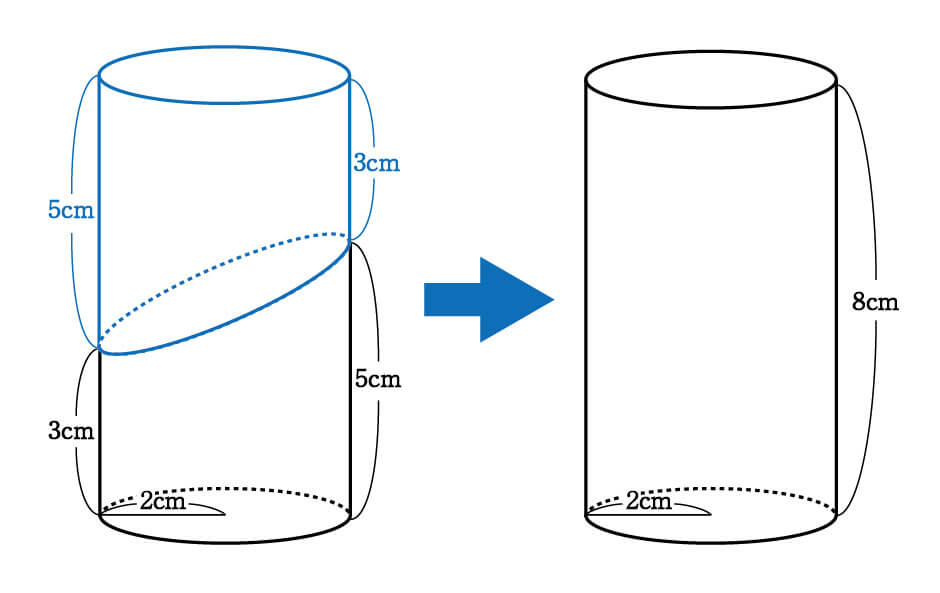
図のように、切頭円柱を反転させて上に乗せると、高さ\(8cm\)の円柱ができます。全く同じ形の切頭円柱が重なっているということは、これを二等分すれば、もとの立体の体積が出せますよね。

 

\begin{eqnarray}4π×（3+5）×\frac{1}{2}= 16π cm^3\\
\end{eqnarray}

 

こういった解き方でも難なく答えが出せますが、公式も覚えておくと良いでしょう。

上の計算式を見てください。これは見方によって、「底面積（\(4π\)）に2つの高さの平均\(（\displaystyle \frac{3＋5}{2}）\)を掛けている」と解釈することもできますよね。

この考え方が、そのまま切頭円柱の体積を求める公式になります。

 

 

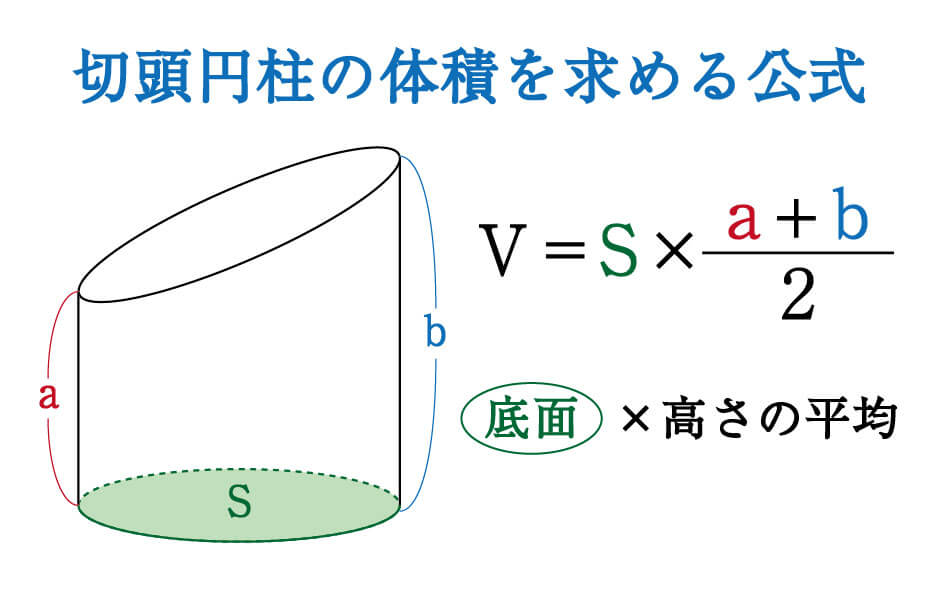
底面積に異なる高さの平均を掛けると体積が出る。この関係を覚えておいてください。

 

ちなみに、この考え方は台形の面積を出す公式と実はよく似ています。

 

上底\(＝a\)、下底\(＝b\)、高さ\(＝h\)という台形があるとしましょう。

この台形を下の図のように、高さ\(＝h\)の辺が底辺となるように\(90°\)回転させてみます。

 

 

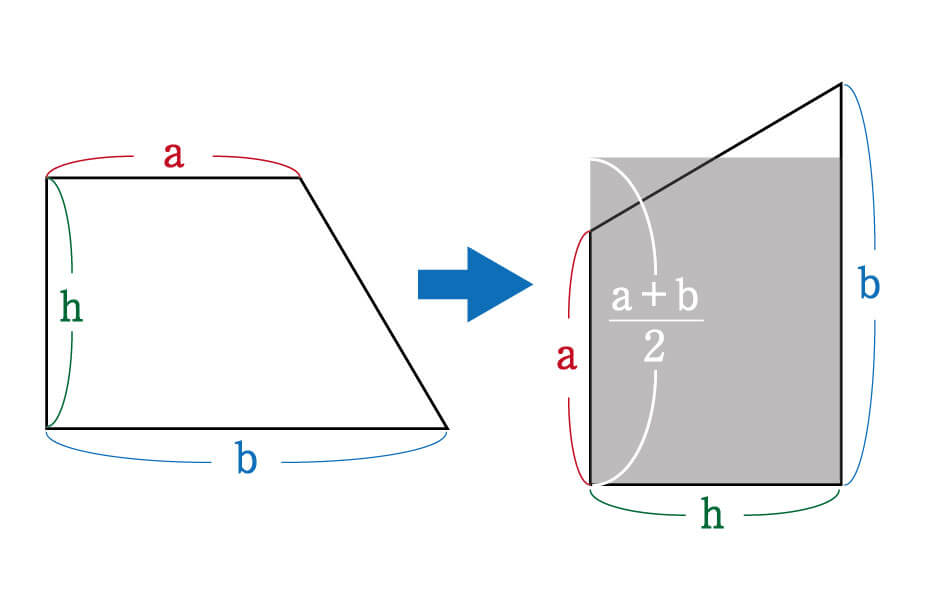
上底\(a\)と下底\(b\)は2つの異なる高さに置き換わったわけですが、両者の平均は（\(\displaystyle \frac{a＋b}{2}\)）という形で表すことができますよね。

この底辺＝\(h\)、高さ＝（\(\displaystyle \frac{a＋b}{2}\)）という長方形（図のグレーで示した部分）の面積は、

 

\begin{eqnarray}h×\frac{a＋b}{2}= \frac{h(a＋b)}{2} \\
\end{eqnarray}

 

と計算することができますが、これは台形の面積を求める公式［（上底＋下底）×高さ÷2］そのままですよね。

 

このように、切頭円柱の体積の公式と台形の面積の公式は、同じような発想に基づいているのです。

 

 

さて、続いては切頭四角柱の問題を見てみましょう。

 

 

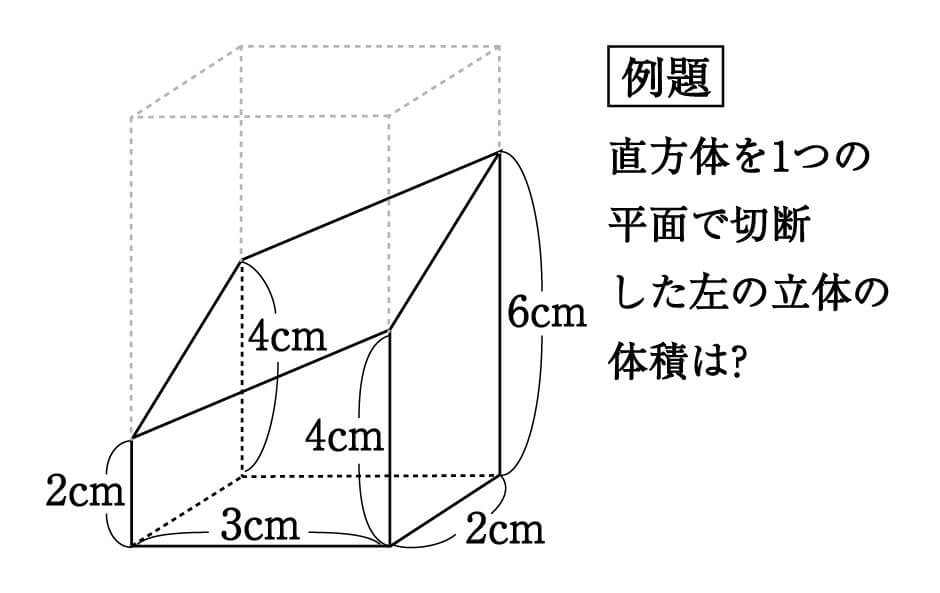
こちらは直方体を斜めに切断した立体の体積を求める問題です。

形は異なりますが、考え方は先ほどの切頭円柱と全く同じ。

底面積に高さの平均を掛けるというやり方で、すぐに答えが出せます。

 

 

公式に当てはめて解いてみましょう。

\begin{eqnarray}（3×2）×\frac{2＋4＋6＋4}{4} = 24cm^3 \\
\end{eqnarray}

 

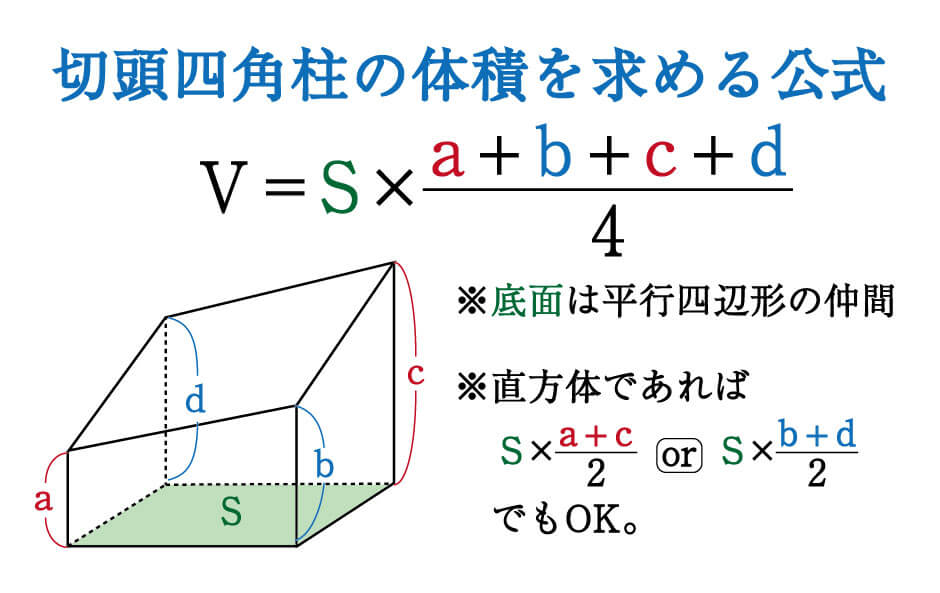
このように、底面が長方形など平行四辺形の仲間である切頭四角柱であれば、時間をかけることなく答えにたどり着けます。

 

なお直方体を切断した立体の場合、図中でいうと\(a\)と\(c\)、または\(b\)と\(d\)の長さの平均は、\(a\)・\(b\)・\(c\)・\(d\)それぞれの長さの平均と等しくなるという性質があります。

よって、直方体に限り、公式中の\(\displaystyle \frac{a＋b＋c＋d}{4}\)　は　\(\displaystyle \frac{a＋c}{2}\)　または　\(\displaystyle \frac{b＋d}{2}\)　に代替可能です。

 

では最後に、トレーニング問題を解いてみましょう。

 

 

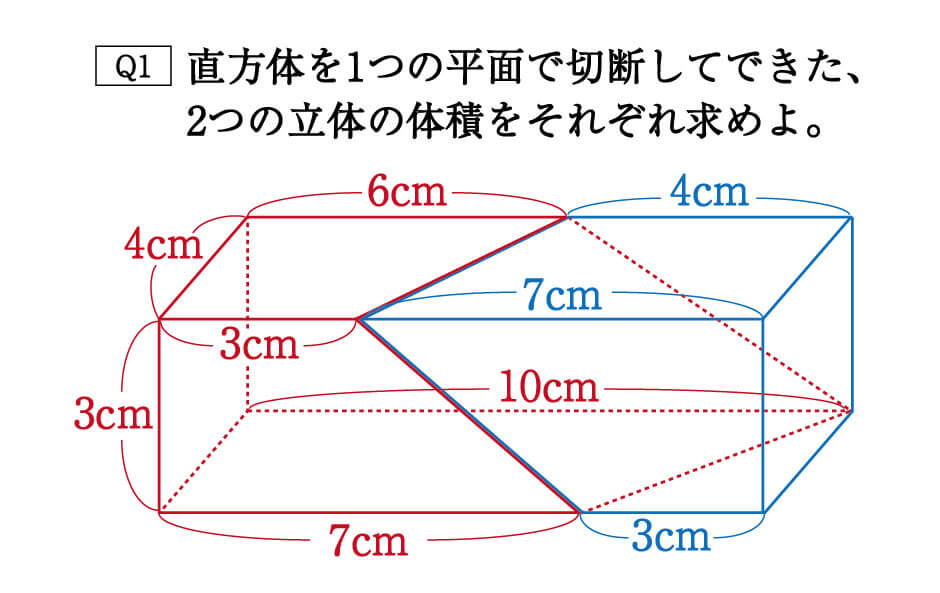
このままでは解きづらいという方は、次のように各立体を分けて考えてみましょう。どちらも先ほどの公式が当てはまる、切頭四角柱であることがわかりますね。

 

 

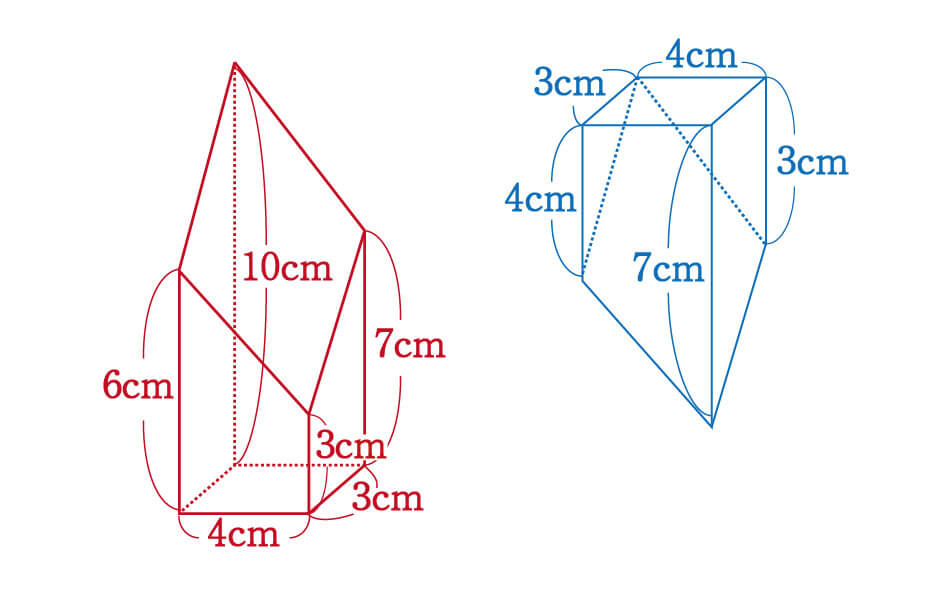
赤い方の体積を\(V1\)、青い方の体積を\(V2\)とすると、答えは以下の通りになります。

\(V2\)のように０が入っていても、問題なく公式が使えるというのがポイントです。

 

\begin{eqnarray}V1＝12×\frac{6＋3＋7＋10}{4} = 78cm^3 \\
\end{eqnarray}
\begin{eqnarray}V2＝12×\frac{4＋7＋3＋0}{4} = 42cm^3 \\
\end{eqnarray}

 

前回の記事 ⇒ 三平方の定理が成り立つ三辺の比：最重要7パターン
次の記事 ⇒ 斜めに切断された三角柱の体積は、こう解くべし!