角度or長さの比を楽に出せるテクニック

今回は角の二等分線が引かれている問題と出会ったとき、必ず思い出せるようにしておきたい公式をいくつか勉強していきましょう。

 

 

1つの角が\(70°\)の三角形があり、底角の二等分線が引かれています。

このとき、2本の二等分線によってできた\(x\)の角度はいくつ?という問題です。

 

まずは正攻法で解いてみましょう。

元の三角形については、次の等式が成り立ちます。

 

\begin{eqnarray}70°＋〇〇＋××＝180° \\
\end{eqnarray}

 

もちろん、この式だけでは〇と×が何度なのかわかりませんが、［〇〇＋××］の値は出せますよね。

 

\begin{eqnarray}〇〇＋××＝180°－70°＝110° \\
\end{eqnarray}

 

続いて内側の青い三角形に注目。

こちらは\(x\)、〇、×という3つの角で三角形が成り立っているので、次のように等式が立てられます。

\begin{eqnarray}x＋〇＋×=180° \\
\end{eqnarray}

 

一見すると、これでは\(x\)の値が出せそうもありません。

しかし、［〇＋×］という部分に着目してみると、これは先ほど計算した［〇〇＋××］の値の半分になるので\(55°\)。

よって、\(x\)の値は次の通りです。

\begin{eqnarray}∠x＝180°－55°＝125° \\
\end{eqnarray}

 

以上が一般的な解き方ですが、やや時間のかかる印象は否めません。

そこで、もっと短時間で答えを出せる方法をお伝えしましょう。

 

手順としては、

①頂角の角度を半分にする

②半分にした角度に90°を足す

という2点のみ。

これならば、5秒で正解が出せるはずです。

 

公式としては、次のように表すことができます。

 

 

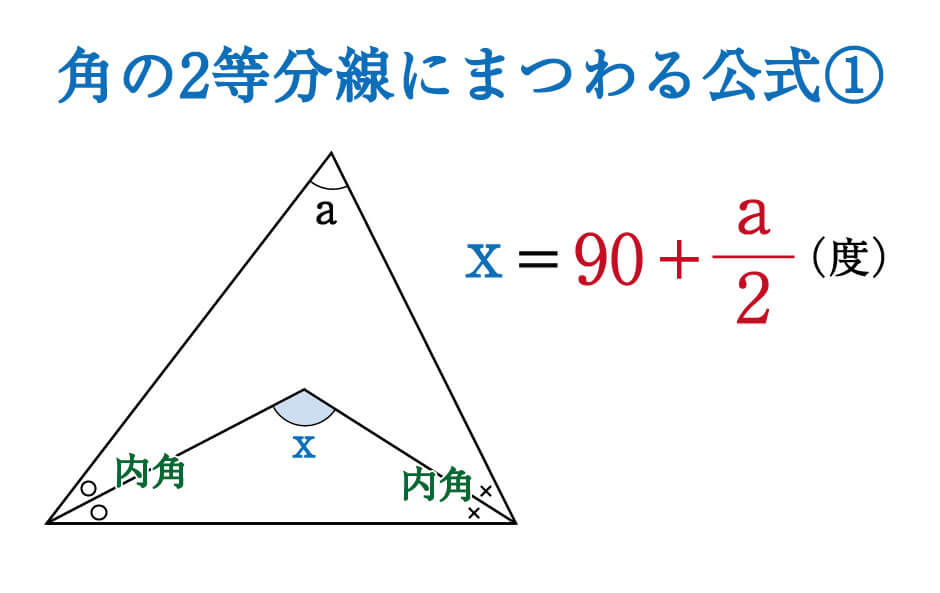
この公式は2つの内角の二等分線によって作られる角の大きさを求めるものですが、内角と外角の二等分線、2つの外角の二等分線という別パターンもあります。これらも、いっしょに覚えてしまってください。

 

 

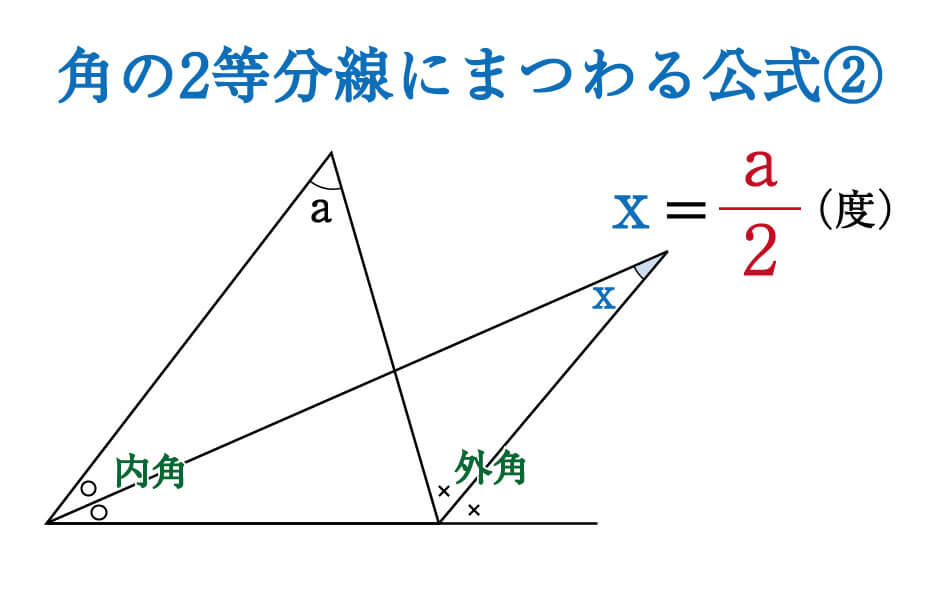
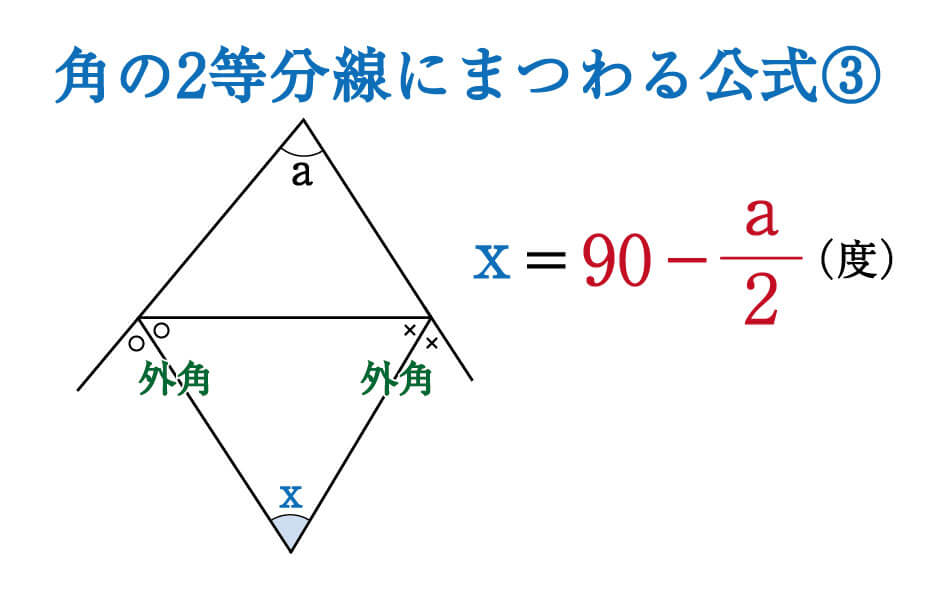
これらの図形が出てきたら、パッと公式が頭に思い浮かぶようにしておきましょう。

 

 

では、もう1つ別のテクニックをご紹介します。

 

 

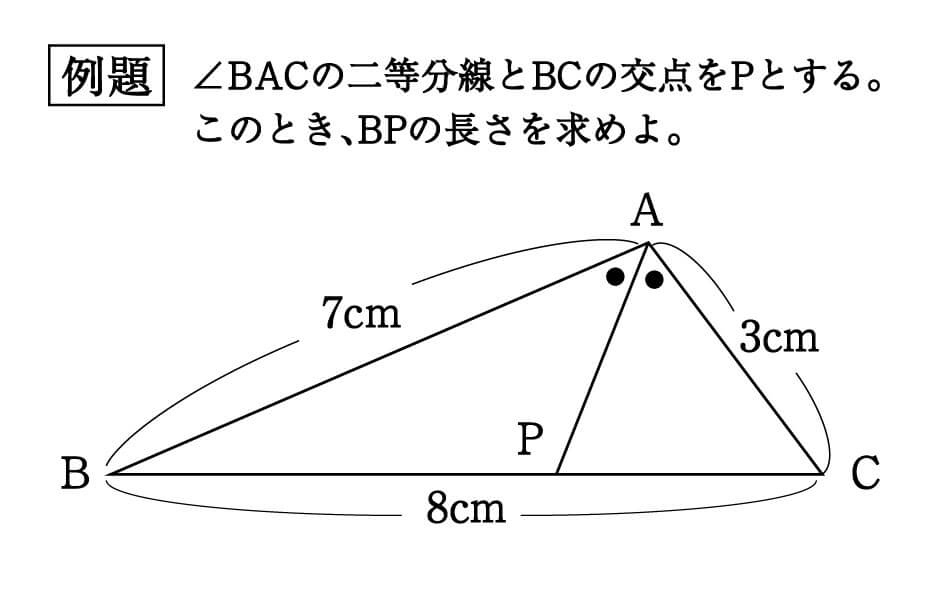
\(7cm、3cm、8cm\)という三辺の△ABCがあり、∠BACの二等分線とBCの交点がPとなっています。

このときのBPの長さはいくつか?という問題です。

 

なぜそうなるのか?という説明は後に回して、先に秒殺テクニックを教えてしまいます。

 

このような図形の場合、二等分されている角を成している二辺（ABとAC）の比の関係が、そのまま二等分線で分けられたBPとPCにも当てはまるのです。

 

つまり、\(BP：PC＝7：3\)となり、BCの長さを10等分した内の7つ分がBPの長さになります。

 

\begin{eqnarray}BP＝8×\frac{7}{10}＝\frac{28}{5}cm\\
\end{eqnarray}

 

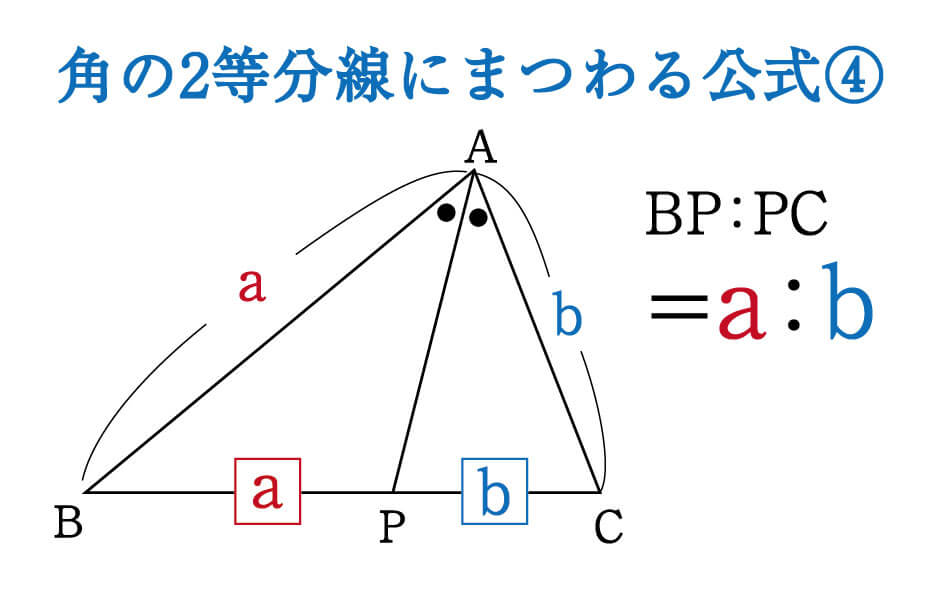
公式として表すと、次のような形になります。

\(BP：PC\)に適応されるのは、あくまでaとbの比の関係である、という点に注意してください。

 

 

では、なぜこの公式が成り立つのか、これから説明していきましょう。

ただし、中学3年生で習う「相似」について知らなければ理解するのが難しい話なので、わからなければ読み飛ばしてもかまいません。

 

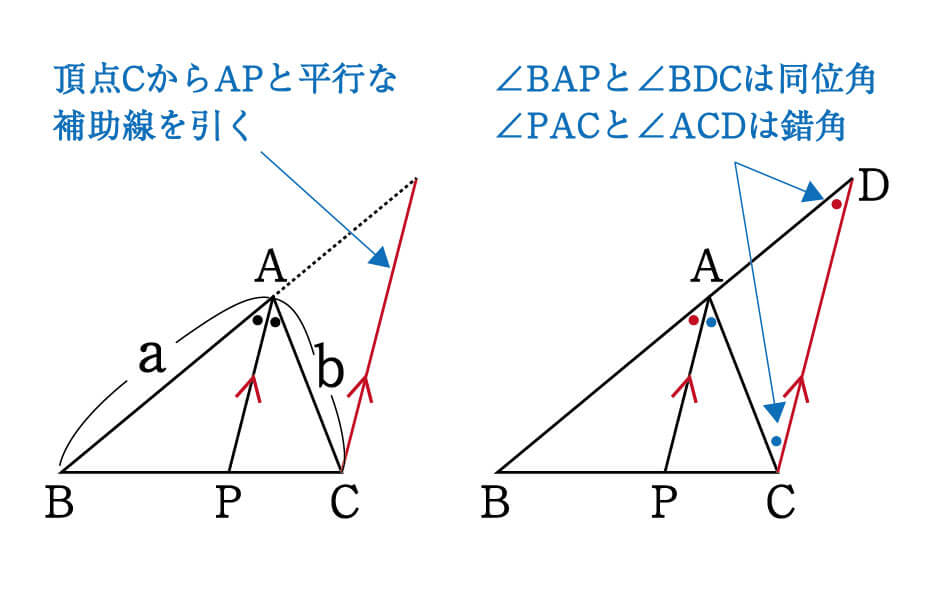
まず、頂点CからAPと平行な補助線を引き、その補助線と辺ABの延長線との交点をDとします。

このとき、∠BAPと∠BDCは同位角（●）のため等しく、∠PACと∠ACD（●）も錯角のため等しいです。

 

 

●と●は同じ角度なので∠ADC＝∠ACD。底角が等しいため、△ACDは二等辺三角形であり、AC＝ADということがわかります。

ここで△ABPと△DBCの関係に注目してください。

 

 

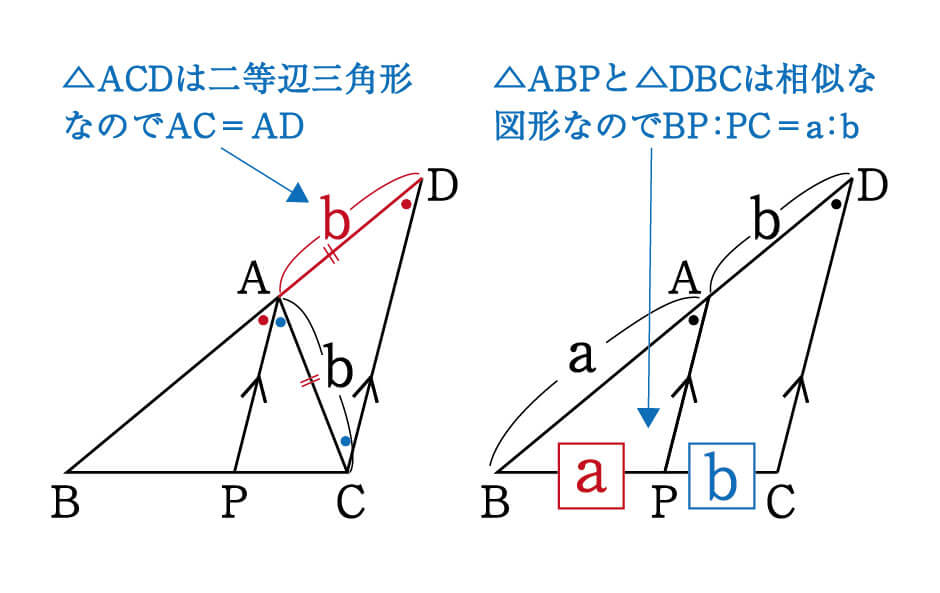
BP：BC=BA：BD＝a:（a＋b） が成り立つことから、BP：PC＝a:bと言えます。（PC＝BCーBPより）
つまり、BA：ADの比をそのままBP：PCに当てはめてOK。
（もちろん、教科書の「平行線と比」のところで学習する「比を平行線に沿って、移すことができる」というテクニックを利用してもOKです）

 

以上が、先ほどの公式を証明する手順です。

もし公式を知らなければ、これと同じ考え方で答えにたどり着かなくてはいけません。

それはかなり大変ですし、そもそも「平行な補助線を引く」という発想が、慣れていなければなかなか思いつくものではありません。

 

そのため、今回の例題のような問題を短時間で解くには、公式を身につけておくことが不可欠なのです。

 

 

では、最後に練習問題でトレーニングしてみましょう。

 

 

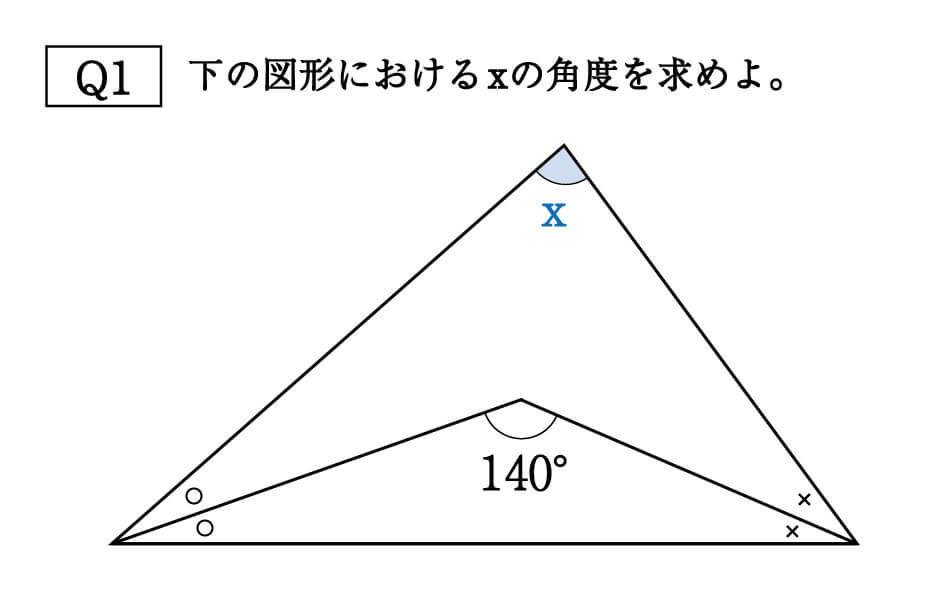
Q1は、公式①とは逆の手順で答えを出すのがポイント。

 

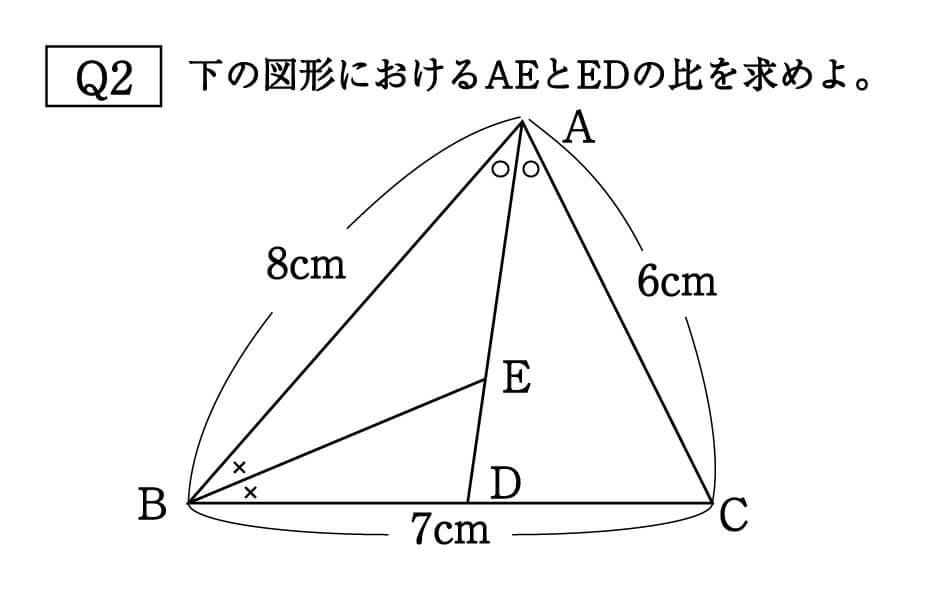
Q2は、\(BA：AC＝BD：DC\)および\(AB:BD＝AE：ED\)という関係が見抜ければ、公式④を使って難なく答えられるでしょう。

 

正解は次の通りです。

 

前回の記事 ⇒ 斜めに切断された三角柱の体積は、こう解くべし!