連立方程式を使わずに短時間で直線の式を求める

 

こういった直線の問題を解くにはいくつか方法がありますが、本記事では5つのレベルにわけて解法を紹介していきたいと思います。

 

 

Lv. 1　2点代入

---

 

\begin{eqnarray}
\left\{
\begin{array}{l}
1＝-a＋b & \\
11=4a＋b &
\end{array}
\right.
\end{eqnarray}
\(y=ax＋b\)という直線の式に、2点の座標を代入する解法です。

おそらく中学生の多くはこの方法で解いていることでしょう。

確実性が高いですし、問題の座標に分数が出てきたときはこの方法が一番効率的です。

ただし、連立方程式を解くことになるので時間がかかりがち。

 

そこで、次の解法を見てみましょう。

 

 

Lv. 2　傾きだけ暗算

---

 

2つの座標\(（-1, 1）\)、\(（4, 11）\)を比べてみると、

\(x\)座標：\(-1→4\)なので差は\(5\)

\(y\)座標：\(1→11\)なので差は\(10\)

ということがわかります。

つまり、この直線の傾きは\(\cfrac{10}{5}＝2\)です。

 

ここまで暗算で出せれば、あとは\(y=2x＋b\)にどちらかの座標の値を代入すればOK。

 

傾き\(＝2\)より \(y=2x＋b\)

⇒\(（4, 11）\)を代入

 

以上の解き方であれば、連立方程式を使わずに済むので、Lv. 1よりも早く答えが出せます。

 

 

Lv. 3　切片まで暗算

---

 

 

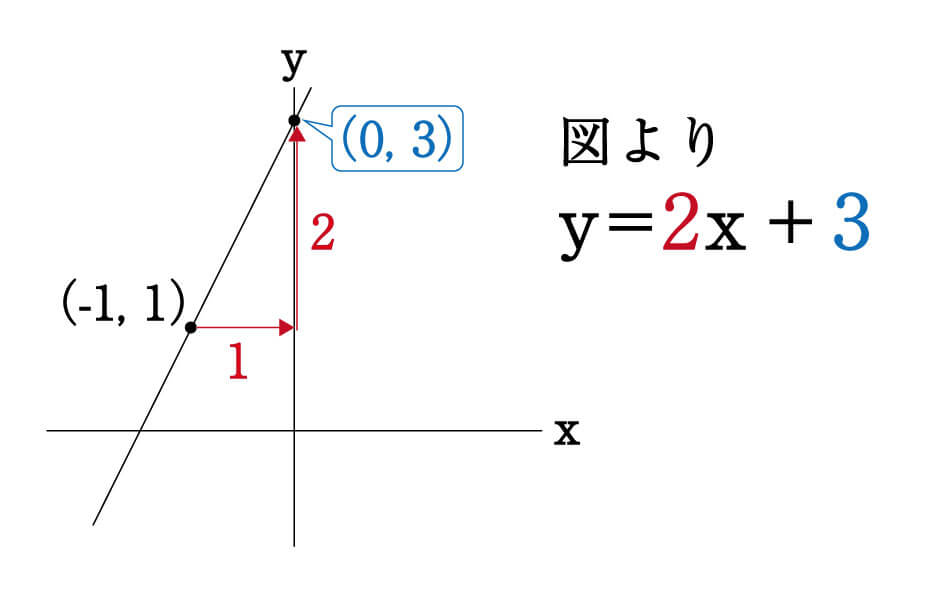
Lv. 1やLv. 2のような代入計算を一切せずに、切片まで出してしまおうという解き方です。

ここでは図を用いてみましょう。

 

\(（-1, 1）\)を通る傾き＝\(2\)の直線は、右に1進んで上に2進んだところ、つまり\(（0, 3）\)にぶつかります。

これはy軸上の点なので、切片は\(3\)ですね。

 

このように図を使えば、面倒な連立方程式や代入計算なしで正解にたどりつくことができます。

 

 

Lv. 4　直線の式を求める公式

---

 

 

Lv. 1～Lv. 3よりもさらに早い解法は、上記の公式を使い一発で答えを出すことです。

中学では教わらない公式ですが、いずれ高校でならうものですし、これを覚えておけば心強い武器になります。

 

では、どれくらい早く解くことができるのか、最初の例題で確かめてみましょう。
 

 

\begin{eqnarray}y=2（x-4）＋11\\
y=2x＋3\\
\end{eqnarray}

 

このように簡単な計算で、パッと答えを出すことが可能です。

 

 

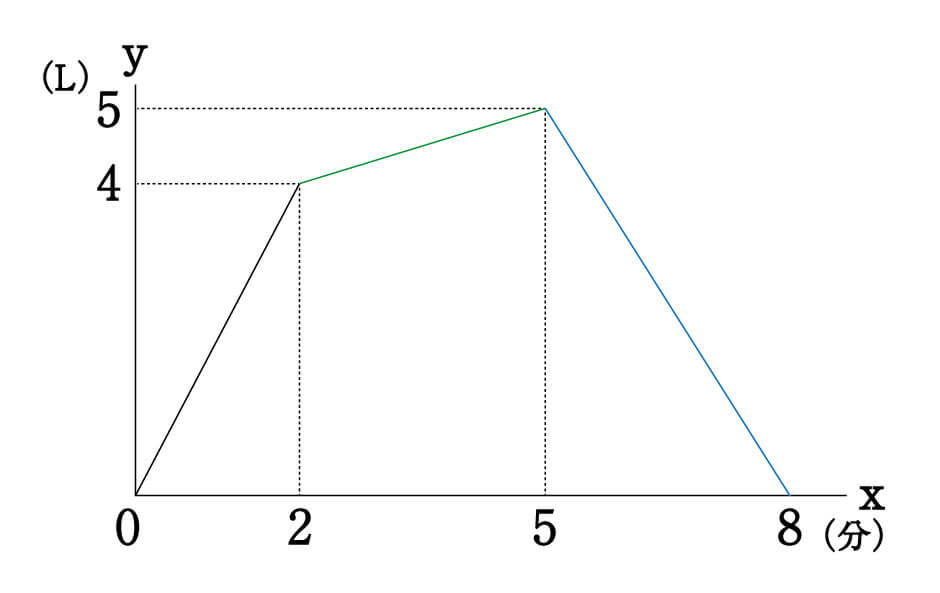
問題によっては、こういったグラフで示された各直線の式を尋ねる問題も出題されます。

 

一番左の直線は単純な比例式なので問題ないですが、真ん中の緑の直線や右の青い直線については、Lv. 1の連立方程式で解こうとするとなかなか大変。

こういったときに、Lv. 4の公式を覚えていればとても有利なのです。

 

緑の直線
 
\(y=\cfrac{1}{3}（x-2）＋4＝\cfrac{1}{3}x＋\cfrac{10}{3}\)
 
青の直線
 
\(y=-\cfrac{5}{3}（x-8）＋0＝-\cfrac{5}{3}x＋\cfrac{40}{3}\)
 
 
さて、続いてはある特定の問題に限って有効なLv. 5の解法を紹介したいのですが、それは次回に説明しましょう。