角度問題の盲点は‟辺のヒント”

 

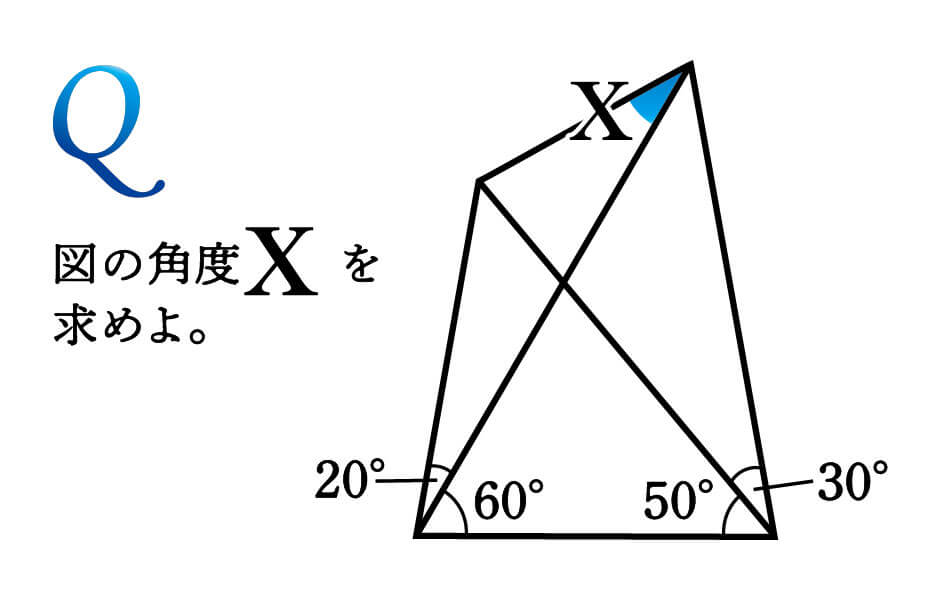
こちらは「ラングレーの問題」と呼ばれる、有名な角度計算の難問です。
与えられたヒントをもとに、いくつか角度を書き足してみましょう。

 

 

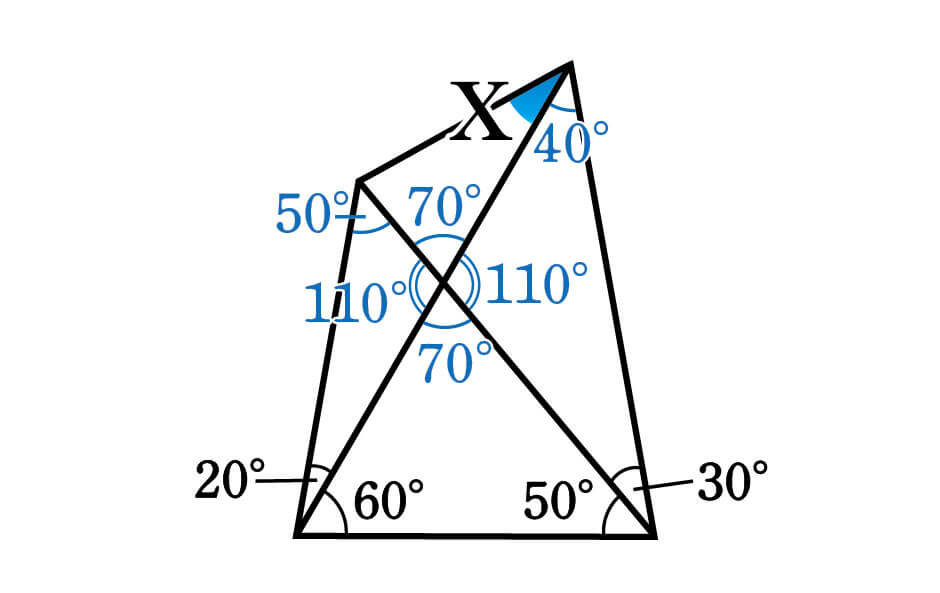
ここで行き詰まってしまった人が多いのではないでしょうか。
ここから先に進めないのは、大事なヒントを見落としてしまっているからです。

 

角度問題では、角に目が奪われがちです。
そのため、他の重要なヒントを見逃してしまい、問題が解けなくなってしまうことがあります。

 

それが「辺のヒント」です。
どうしても角度問題が解けないという場合は、盲点になりがちな辺に目を向けてみてください。

 

ラングレーの問題を見直してみましょう。
すると、次のように底角がそれぞれ50° の二等辺三角形（△ABC）を見つけることができます。

 

 

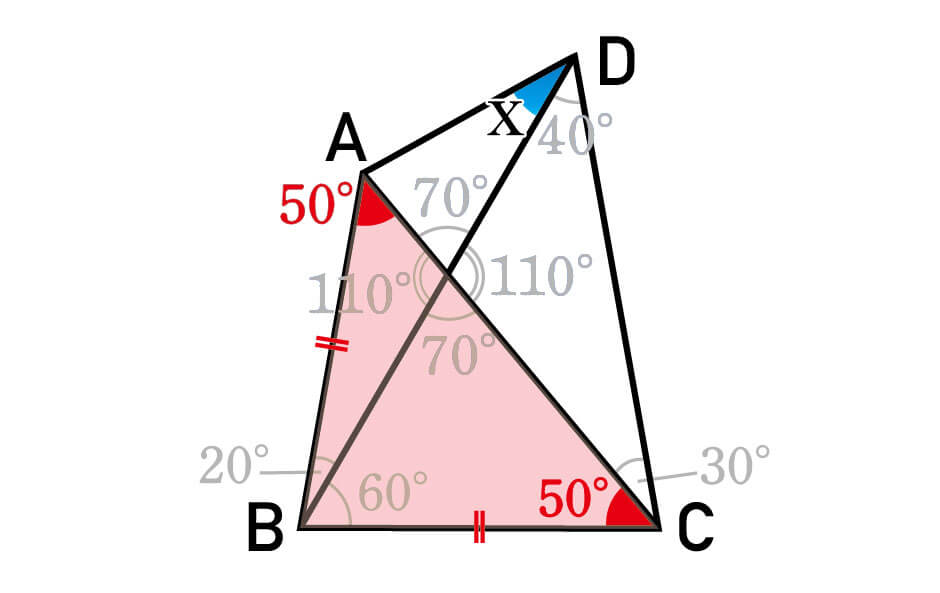
ここで得られたAB＝BCという情報が、ラングレーの問題を解くための大きなカギです。
先に結論を言ってしまうと、正解するには、この図の中にあと3つ同じ長さの線が必要になります。

 

ここから先は、試行錯誤していきましょう。
辺AB・辺BCと等しい長さの線を探しても、この状態のままでは見つかりません。
そのため、図の中に補助線を引くことで新たなヒントを導き出します。

 

狙うべきは、補助線によって新しい二等辺三角形を作り出すこと。それにより、角度の情報を増やしていきます。

 

次の一手を思いつくのはかなり難しいのですが、角度が60°の∠DBCに着目してみましょう。
これを20°と40°に分割する線を、頂点Bから辺CDに向かって引きます。

 

 

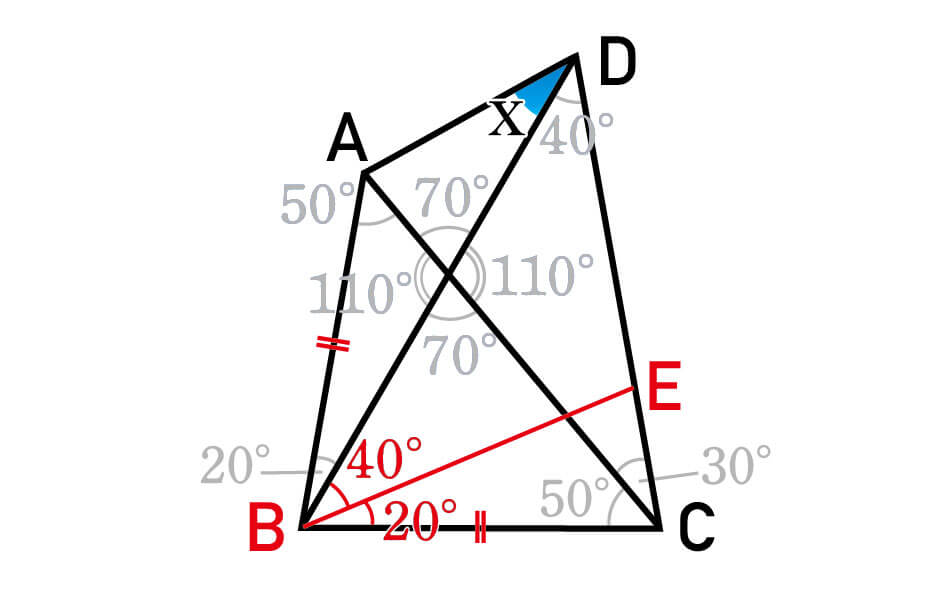
なぜここに補助線を入れたかというと、この1本によって新しい二等辺三角形を同時に2つも作り出せるからなんです。

 

補助線とCDの交点をEとします。このとき、△BCEを見てみると、∠EBCが20°、∠BCEが80°（50°＋30°）です。三角形の内角の和が180°であることから、∠BECも80°だとわかります。
よって、△BCEはBC＝BEの二等辺三角形です。

 

続いて△BDEですが、こちらも見ての通り底角40°の二等辺三角形です。

 

 

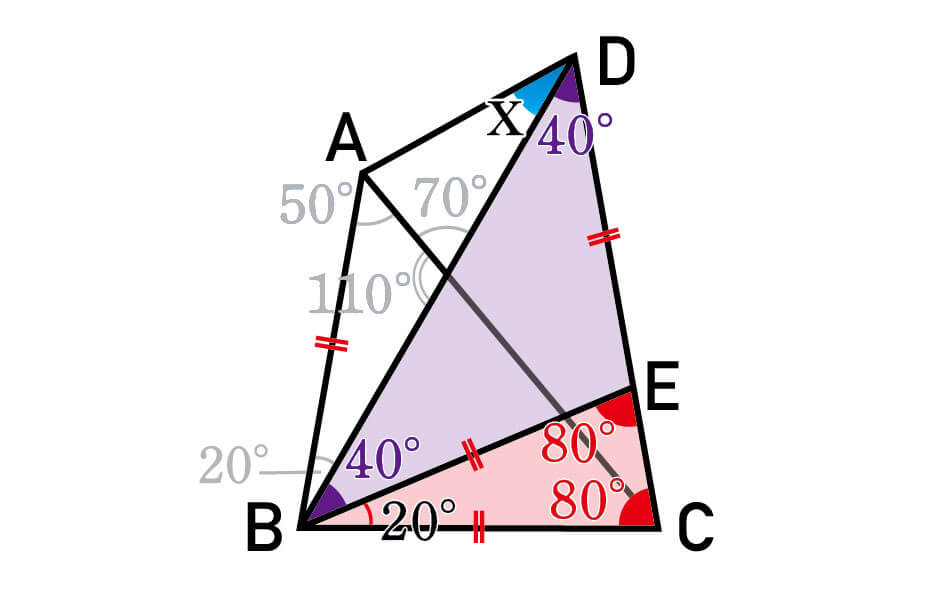
このように補助線は、1本引くだけで倍のヒントが得られる、一粒で二度おいしいようなものを目指していきましょう。

 

さて、正解にたどり着くには、辺AB・辺BCと同じ長さの辺を3つ増やせばいいので、残り1本です。

 

ヒントを出しましょう。
注目してほしいのが、先ほどの補助線でできた∠ABE。
20°＋40°＝60°の角を、うまく使えないか考えてみましょう。

 

では、最後の補助線を引きます。答えはAとEを結ぶ線です。

 

 

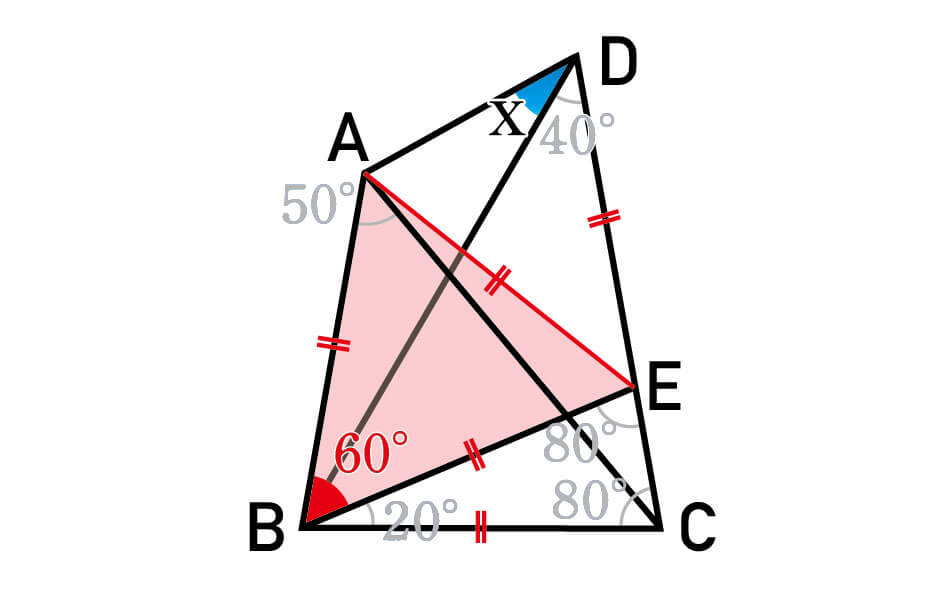
これにより頂角が60°、BA＝BEの二等辺三角形BAEができます。
ただ、頂角60°の二等辺三角形とはつまり正三角形のことですよね。
そのため、いま引いた補助線AEは、BAおよびBEと等しい長さだと言えます。

 

これで補助線は揃いました。ここまでに得た情報を整理した図がこちら。
問題の角度Xを含む三角形をよ～く見てみましょう。

 

 

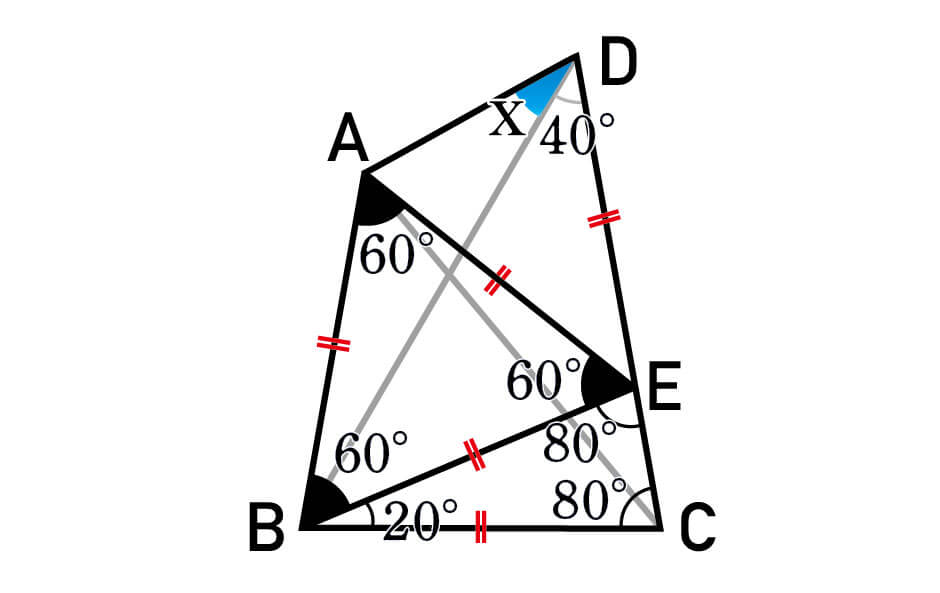
△EADがEA＝EDの二等辺三角形であることに気がつけば、正解まであと少し。
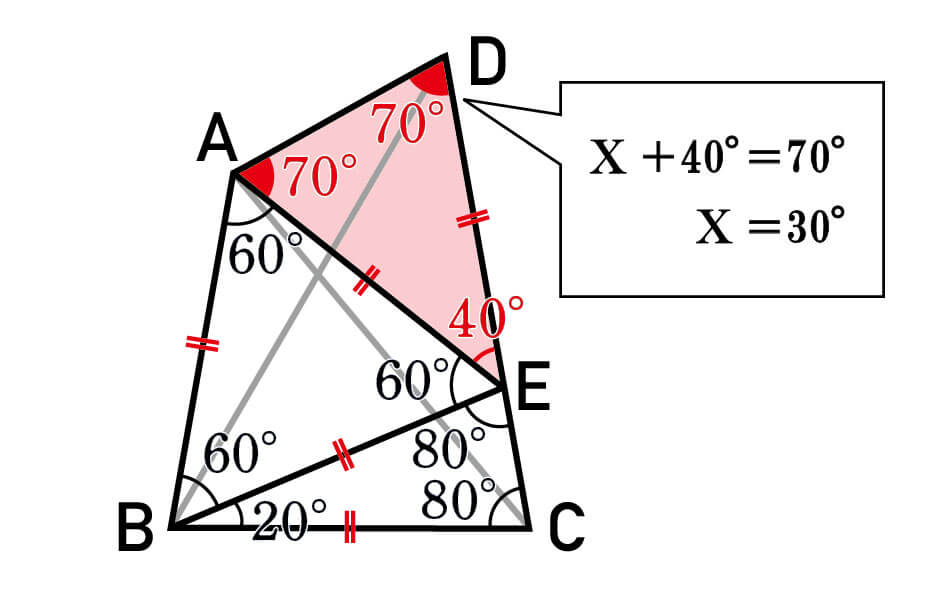
∠BEC＝80°、∠AEB＝60°なので
\begin{eqnarray}
∠AED＝180°－（80°＋60°）＝40°
\end{eqnarray}
頂角が40°である二等辺三角形EADの底角は
\begin{eqnarray}
（180°－40°）÷2＝70°
\end{eqnarray}
∠ADEはXと40°を足して70°になるはずなので
\begin{eqnarray}
X＝70°－40°＝30°
\end{eqnarray}
正解は30°です。

 

 

いかがでしたか。はじめてこの問題に挑戦して、なんのヒントもなく必要な補助線を引くことはかなり難しいでしょう。
「そんなトリッキーな補助線、思いつけない！」と思う人もいるでしょう。

 

ただ、今回の補助線は闇雲に引いたものではなく、「二等辺三角形を作る」という明確な狙いを持っていたからこそ見つけられたものです。
また、1本の補助線で複数の新しいヒントを導き出すよう意識するのも大切。
これから角度問題に取り組むときは、これらのポイントを踏まえて臨んでみましょう。