関数の難問を等積変形で解く

 

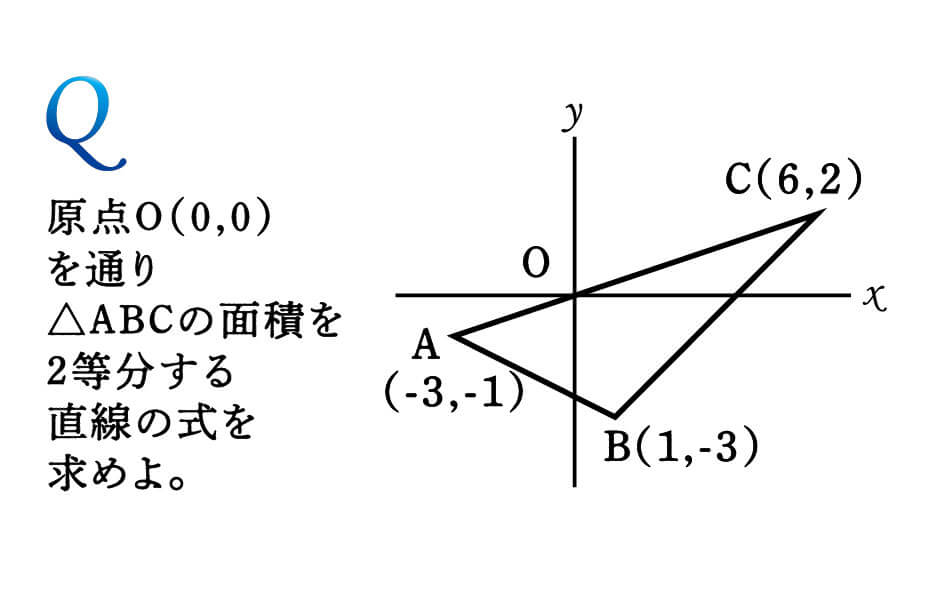
「面積を2等分する直線の式を求めよ」というのは、関数の問題では有名なパターンです。
ただ、今回の問題は辺AC上に原点Oがあるというのが厄介なポイント。

 

まずは、「正解の直線はだいたいこんな感じかな」という線を入れて、完成予想図を作ってみましょう。
そうすると、次のような右下がりの線になると思います。

 

 

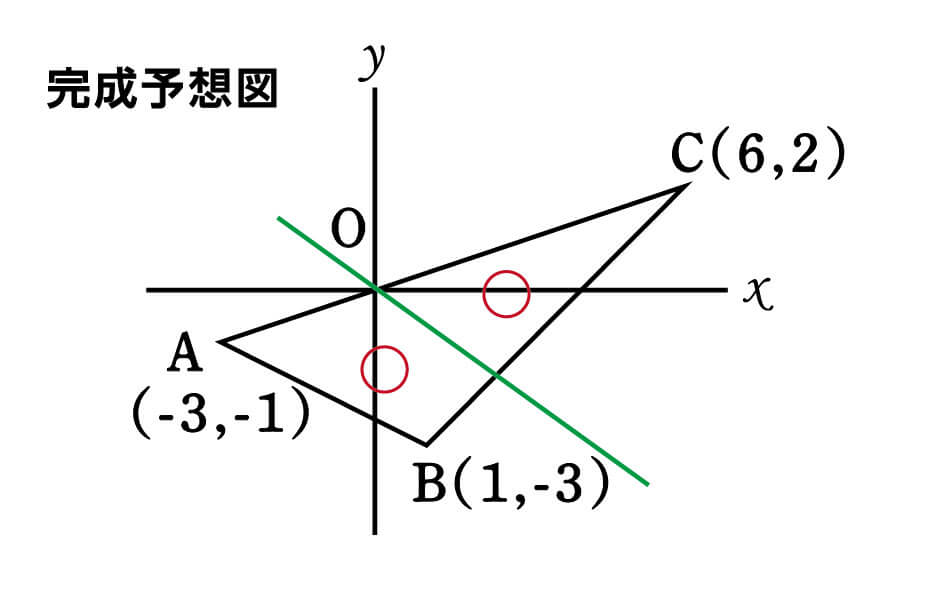
△ABCが緑色の線によって三角形と四角形に分割されていますが、このような形の面積二等分のパターンは、経験が少ないのではないでしょうか。

 

もっとも基本的な三角形の面積2等分の解法は、以下のように頂点と底辺の中点を通る直線を引いて解くパターンです。

 

 

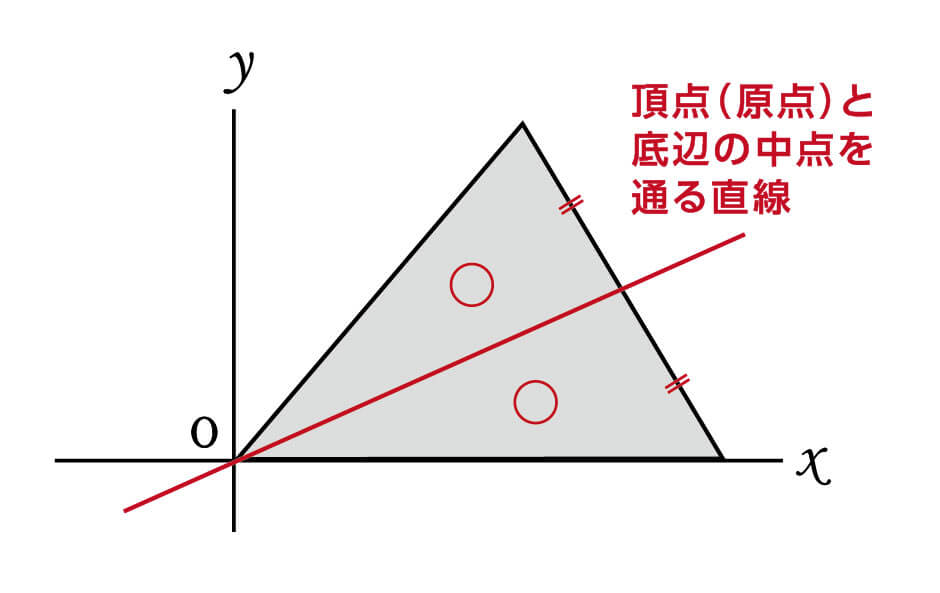
こちらは何度も解いているという人も多いはず。
しかし、今回の問題はこの有名なパターンとは違う形です。

 

では、どうすれば解けるのか。
解法はいくつかありますが、ここでは等積変形のテクニックを使った方法を紹介します。

 

△ABCを変形することで、何とか「頂点と底辺の中点を通る直線」で解くことができないか、という考え方です。
次のように、Oを頂点とする△ABCと同じ面積の△ORCを作り出し、底辺の中点Pを求めます。

 

 

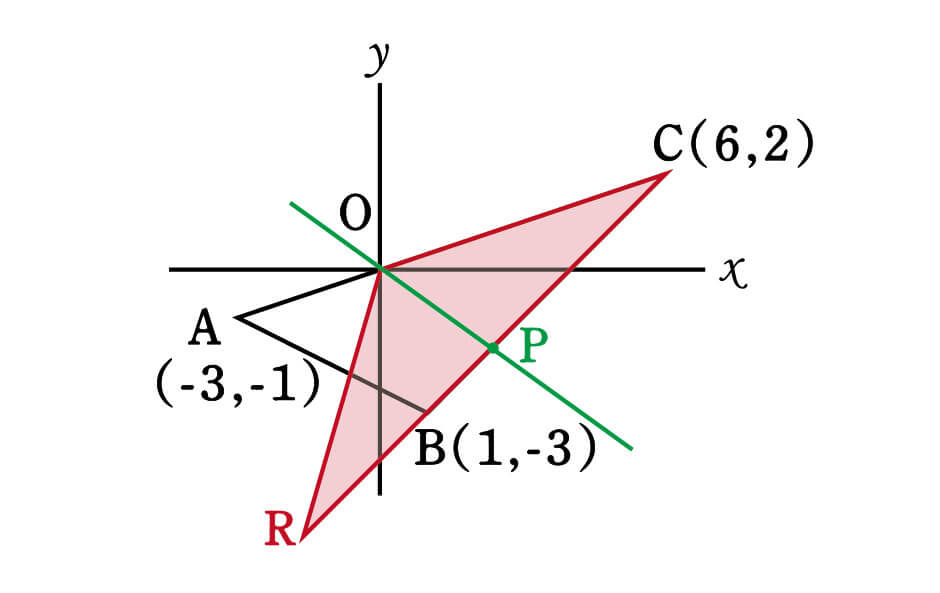
頂点OとPを通る直線の式を求めれば、それが△ABCを2等分する直線の式になるというわけです。

 

ではここで、下の図を用いて等積変形の手順を説明していきます。
BPの延長線上に点Rを取り、四角形OABPと同じ面積を持つ△ORPを作図してみましょう。

 

 

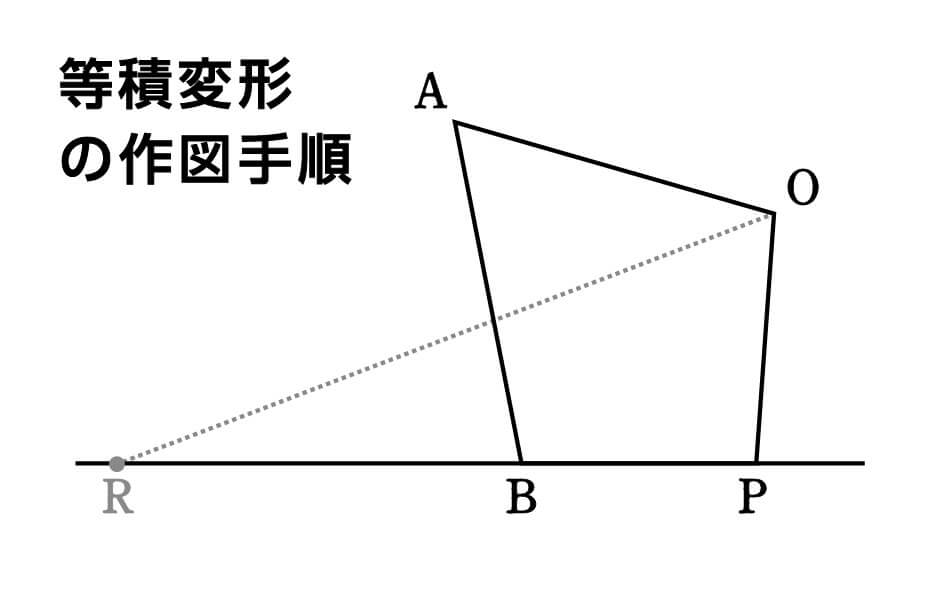
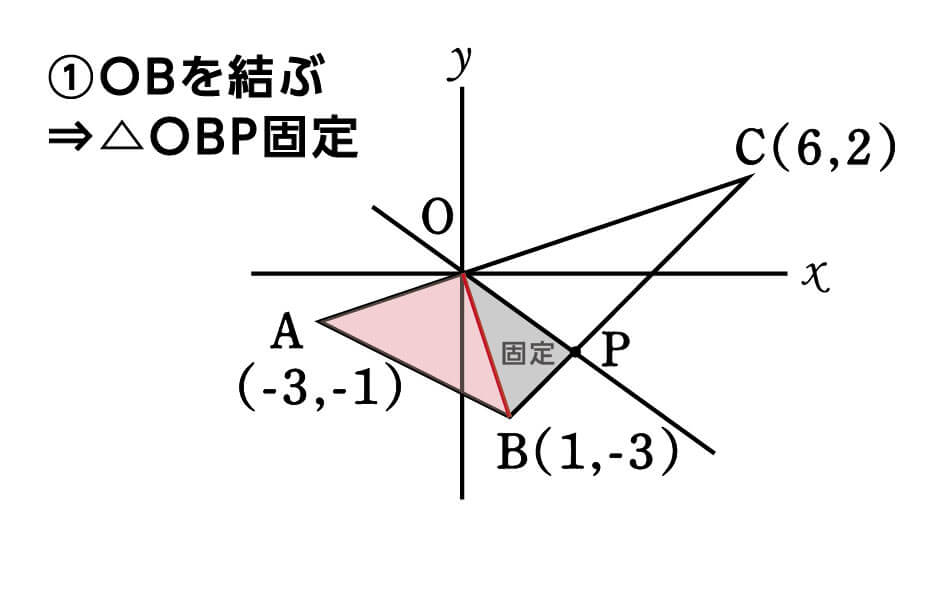
まず、OとBを線で結びます。
これによって、四角形OABPが△ABOと△OBPに分割されました。

 

 

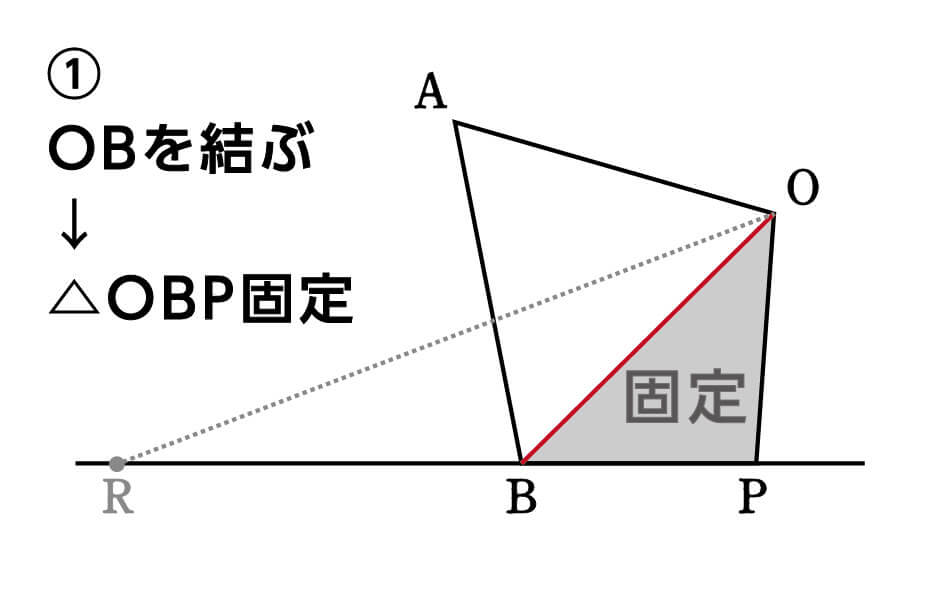
このとき、まだRの位置は定まっていませんが、△ORPに注目してみましょう。
すると、こちらにも△OBPが含まれていることがわかりますね。

 

△OBPは共通なので、面積は変わりません。
よって、ここを固定してしまえば、四角形OABPを変形するのではなく、△ABOを△ORBに変形すれば良いという方針が定まります。

 

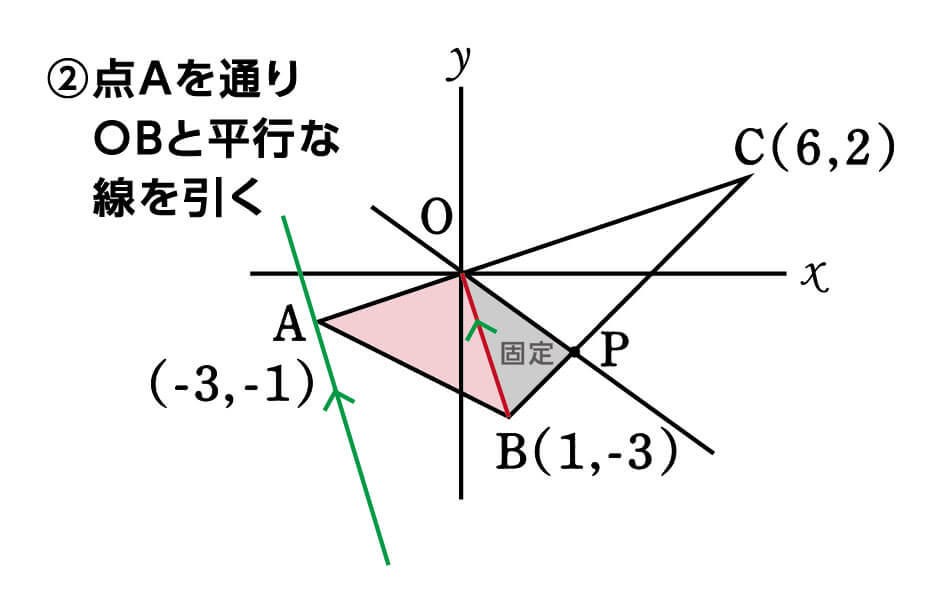
続いて、OBと平行で、かつ頂点Aを通る直線を引いてみましょう。

 

 

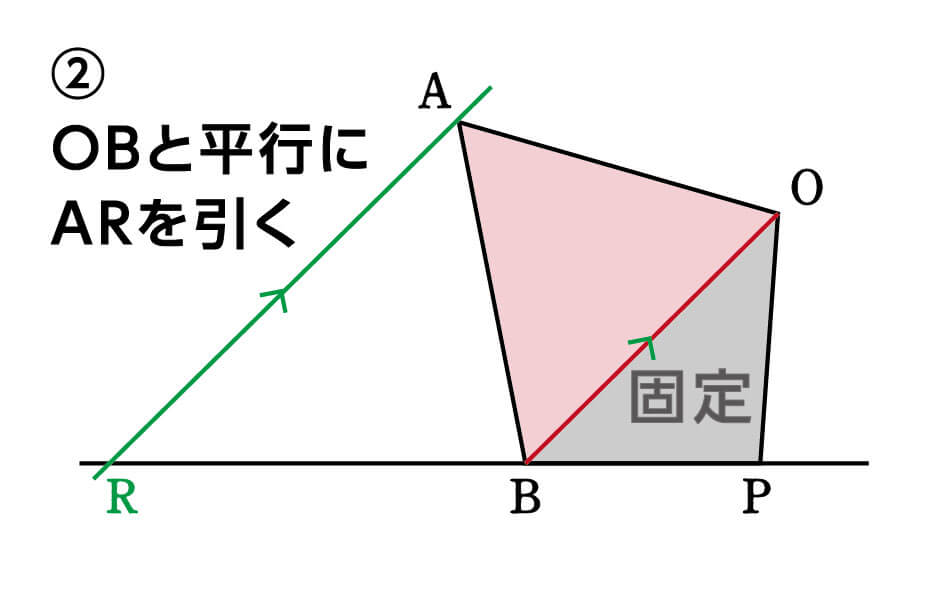
この直線上であれば、頂点Aをどこに動かしても高さが等しく底辺の長さも等しい、つまり面積が同じ三角形を描くことができます。
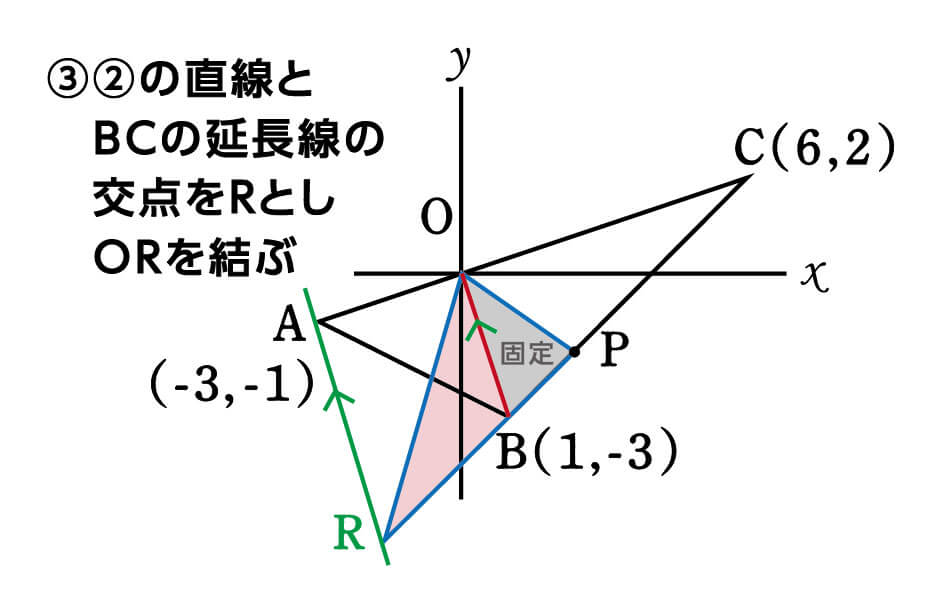
ということは、この直線とBPの延長線の交点が、求めていたRになるということです。

 

 

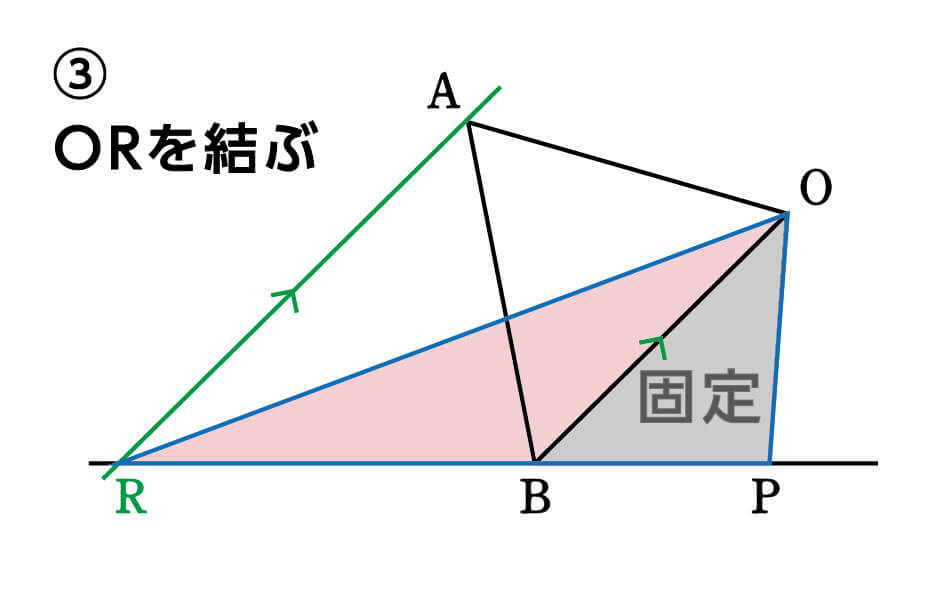
これで面積を変えずに、四角形OABPを△ORPに変形させることができました。
このテクニックを、今回の面積2等分の問題にも当てはめてみましょう。

 

 

△OPCは元の△ABCにも変形後の△ORCにも含まれる、共通部分です。
よって、△OPCに手を加える必要はないので無視します。

 

変形しなくてはいけないのは、四角形OABPの方です。
ここからの手順は、先ほどの等積変形の例と全く同じ。
次のようにして四角形OABPを△ORPに変形させましょう。

 

 

これで元の△ABCと面積が等しい、△ORCを作図することができました。
あとは関数の知識で、面積2等分の直線の式を求めることができます。

 

まず、Rの座標を求めましょう。
RはARとCRの交点ですから、2つの直線の式の連立方程式によって求めることができます。

 

直線ARの傾きは、平行線であるOBと同じです。
直線OBを見てみると、原点と（1, -3） を通る直線なので、傾きが-3とわかります。
よって、直線ARの式は\(y=-3x+b\)と表すことができます。
この式にA（-3, -1）の座標を代入することで、切片を出しましょう。

 

\begin{eqnarray}
y&=&-3x+b ←（-3, -1） \\
-1&=&9+b \\
b&=&-10 \\
\end{eqnarray}

 

傾きが-3、切片が-10なので、直線ARの式は\(y=-3x-10\)です。

 

続いて、直線CRの式ですが、CとBの座標がわかっているので、それぞれの値を代入すれば\(y=x-4\)だとわかります。

 

あとは、2つの式を連立方程式で解くだけ。

 

\(\left\{\begin{array}{l}y=x-4\\y=-3x-10\end{array}\right.\)

 

Rは\(（-\cfrac{3}{2}, -\cfrac{11}{2}）\)です。

 

 

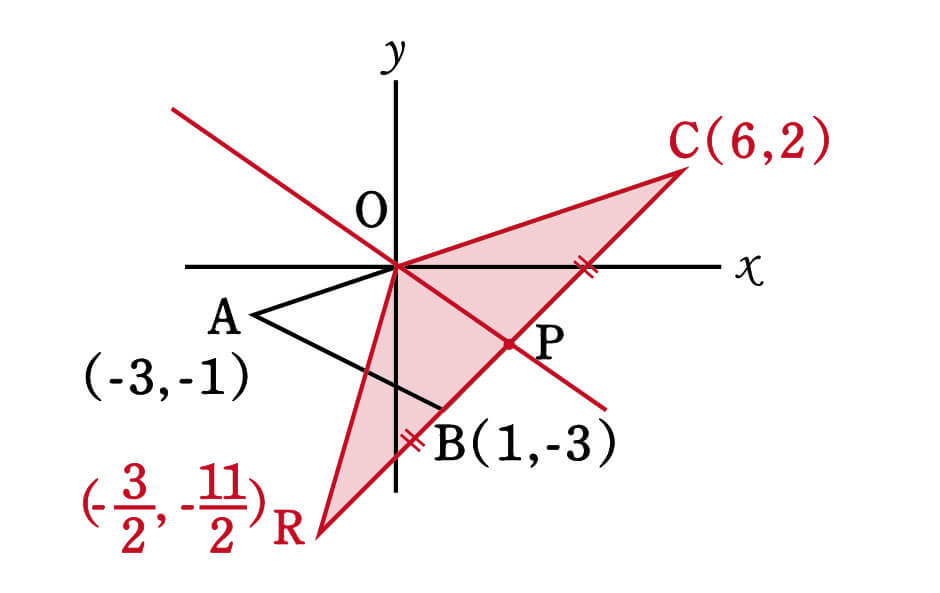
Rの座標がわかったので、RとCの中点Pを求めれば、△ORCを二等分する直線OPの式がわかります。
 
中点は各座標の平均で出すことができるので、x座標、y座標をそれぞれ足して2で割ればOK。

 

\begin{eqnarray}
&x&座標（-\cfrac{3}{2}+6）÷2=\cfrac{9}{4} \\
&y&座標（-\cfrac{11}{2}+2）÷2=-\cfrac{7}{4} \\
\end{eqnarray}

 

中点Pの座標は\(（\cfrac{9}{4}, -\cfrac{7}{4}）\)です。
これを比例式\(y=ax\) に代入して、答えを出しましょう。

 

正解は\(y=-\cfrac{7}{9}x\) でした。