円すいを速攻で展開する方法

高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる“秒殺テクニック”を紹介していきます。

 

円すいの問題はよく出題されます。

例えば、母線が12cm、底面の半径が3cmの円すいがあるとしましょう。これを展開した時にできる、側面のおうぎ形の中心角は何度になるでしょうか？

 

 

まずは一般的な方法で解いてみましょう。

底面の半径が3cmなので、円周＝直径×\(π\)＝6\(π\)cmとなります。底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6\(π\)cmです。

そこから、半径12cm＆孤の長さ6\(π\)cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。

 

このやり方では、ちょっとした方程式も出てくるので、早い方でも20秒、ゆっくり解くと1分かかることもあるでしょう。入試本番では、それほど時間をかけてはいられません。

 

ここで秒殺テクニックの紹介です。

 

結論からいうと、円すいを開いた時にできるおうぎ形の中心角は、母線と底面の半径の関係で決まってしまいます。

そのため、母線の長さをR、底面の半径をrとした場合、以下の公式が成り立ちます。

 

 

例題に当てはめてみると、このようになります。

 

 

 

この公式を使えば、かなりのスピードで正解にたどり着けますが、それでも8秒くらいはかかるでしょう。

 

では、5秒で解くにはどうしたら良いか。

そのためには以下の手順で解いてください。

 

① \(\frac{r}{R}\) という分数を作る。

② 約分する。

③ 角度変換する。

 

角度変換とはどういうことか。例えば、\(\frac{1}{4}\)という分数を見て、円を四等分したものを想像し、90°という中心角を瞬間的に導き出すこと。

これが角度変換です。

 

最初の問題を使って復習してみましょう。

 

このテクニックによって5秒で解くことができます。

それでは、5つの円すいでトレーニングしてみましょう。

 

 

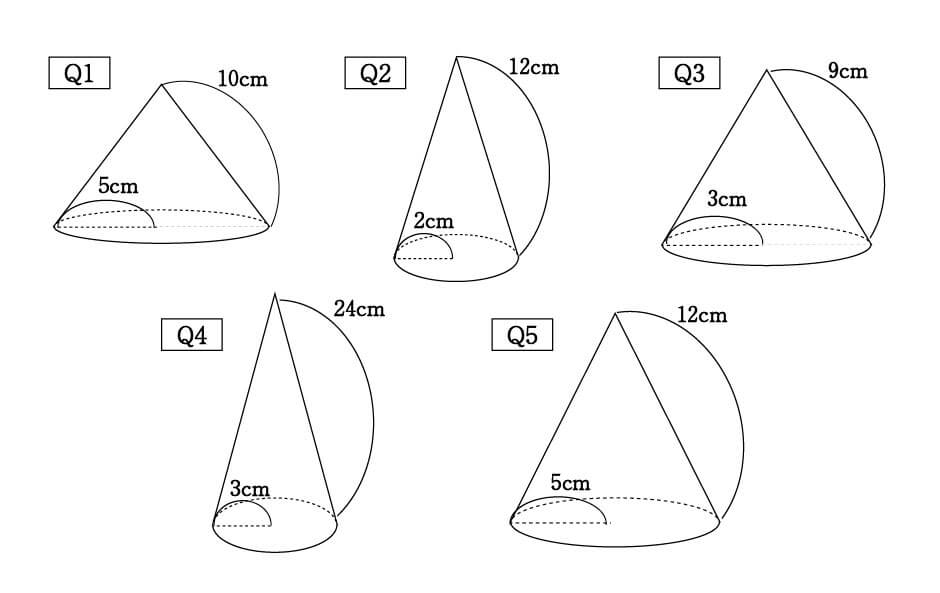
正解はこちらです。

 

Q1～Q4は、約分した分数を見て、即座に中心角が答えられるようにしておきましょう。

 

Q5のような瞬間的に角度が思いつきにくい分数については、公式に当てはめて8秒以内に解答できれば問題ありません。

 

次の記事 ⇒ 三角錐の体積比を楽に求められる公式