補助線いらずの「メネラウスの定理」

高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる“秒殺テクニック”を紹介していきます。

今回紹介する“メネラウスの定理”は、中学3年生の授業ではほとんど教えてもらう機会のない、高校1年生の内容です。しかし、使えるようになるとすごく便利なので、中3のうちから習得しておくのがオススメ。

参考書などには載っていることも多く、メネラウスの定理があることを知っている中3生は少なくありませんが、経験上「使えない」という生徒がほとんどです。そのため上手く活用するためには、トレーニングが欠かせません。

今回の講義を通して、しっかり自分のものにしましょう。

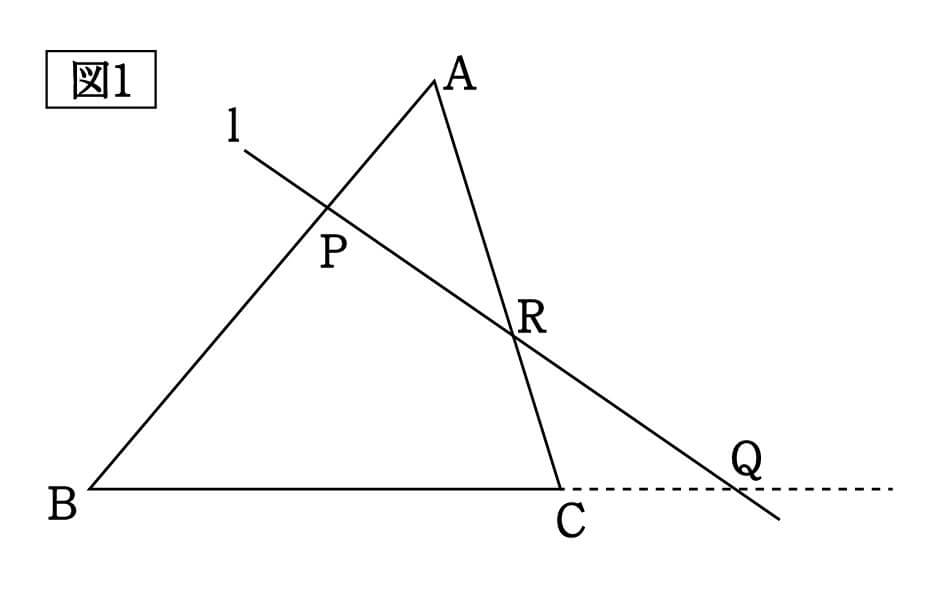
図1のような図形があり、いくつかヒントが与えられた状態でCR：RAの比を問われているとしましょう。

辺の比を考えるときには、相似が便利です。しかし、ここには相似な関係の図形がないため、補助線を引かなくてはいけません。平行線を引いて、よくある相似の形を作り出す、それが解答する上でのカギになります。

ただし、メネラウスの定理を使えば、こういった問題でも補助線を引くことなく解けるようになるのです。

図1の状態を確認してみましょう。△ABCがあり、それを直線lが貫いています。lは辺AB、AC、およびBCの延長線と交わっており、それぞれの交点をP、R、Qとなっている。

ここに、ある1つの等式が成り立ちます。それがメネラウスの定理です。

具体的にどんな等式なのかは後述しますが、まず重要なのは「いつメネラウスの定理が使えるのか？」ということ。それは、問題となっている図形に、下の「キツネさん」の形があるときです。

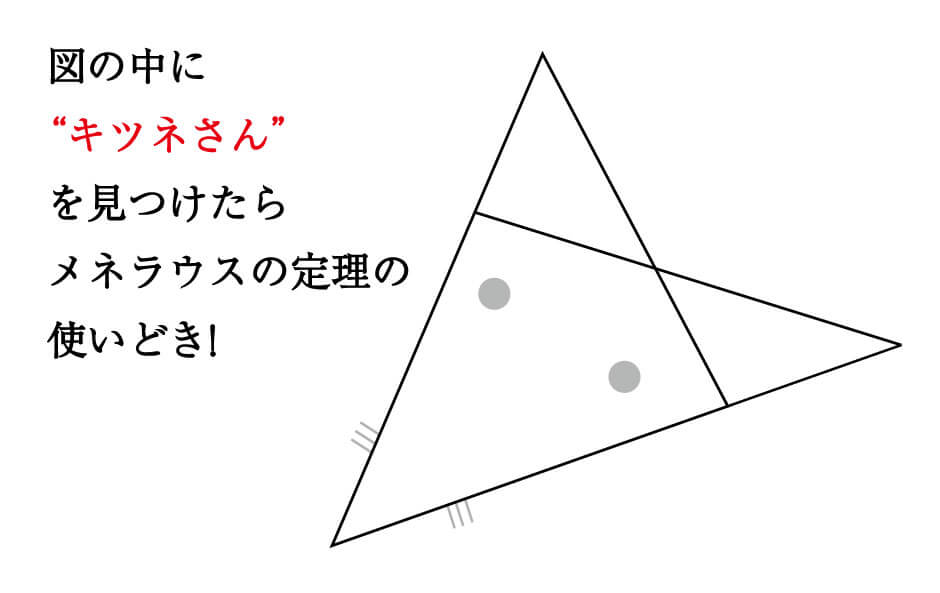
問題によっては、メネラウスの定理が使えるのかわかりにくい図もあります。「キツネさんが出てきたらメネラウスで勝負!」という感覚を、持っておきましょう。

また、メネラウスの定理はかなり変てこな公式なので、丸暗記するのが難しいです。そのため、公式を憶えるための“イメージ”を事前につかんでおくことが重要となります。そのイメージについて説明しましょう。

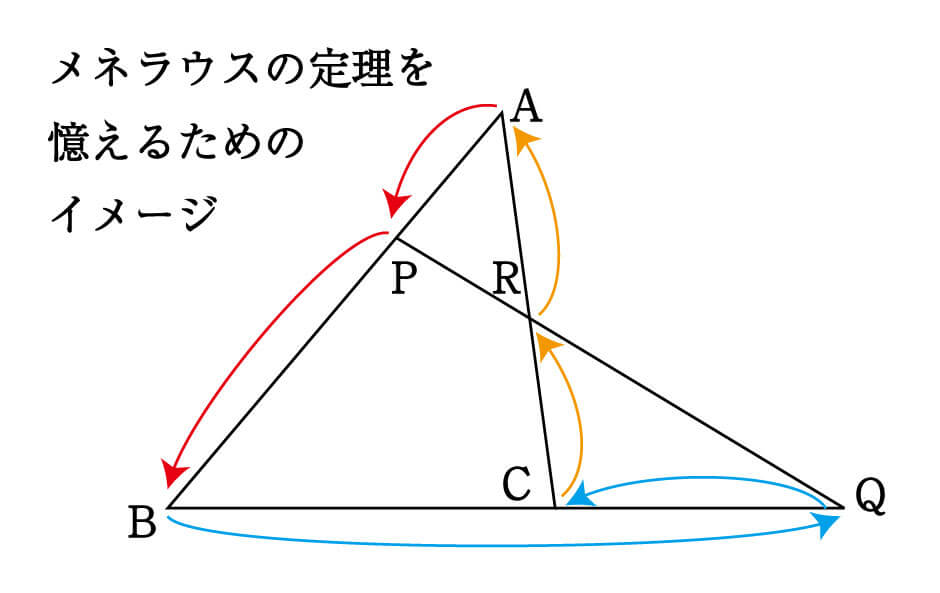
まず、△ABCの周りをグルッと1周する、と考えてください。A→B、B→C、C→Aと順番に“旅”をしていきます。ただし、この“旅”にはルールがあります。

A→P→B、B→Q→C、C→R→A

このように、必ず寄り道をしてください。これを踏まえて、実際の公式を見てみましょう。

これを「ただ暗記しなさい」と言われると、「えっ、ちょっと無理…」となりがちですが、先ほどのイメージを持っている皆さんは、既にこの公式を憶える準備が整っています。

実は、先述した“旅のルール”が、メネラウスの定理を憶えるための最大の秘訣なのです。

旅のルートは①AP ②PB ③BQ ④QC ⑤CR ⑥RAです。この順番で分子→分母と当てはめていき、3つの分数をかけたもの＝1とすれば、メネラウスの定理ができ上がります。

それでは、実際にこの公式を使ってみましょう。

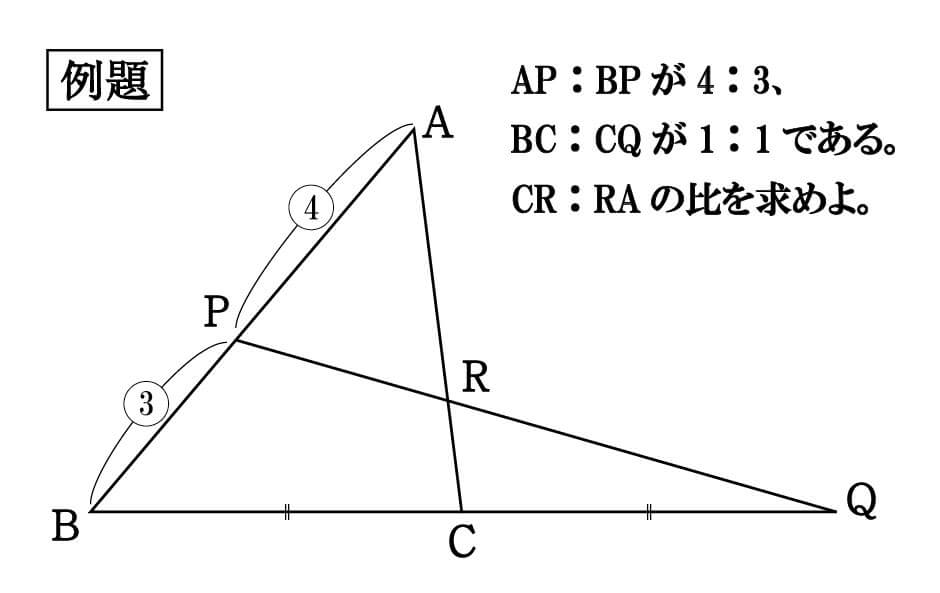
前述したように、メネラウスの定理を使えば、この手の問題でも補助線は必要ありません。

答えは\(CR：RA＝3：8\)。

続けて、同じような問題で練習しましょう。

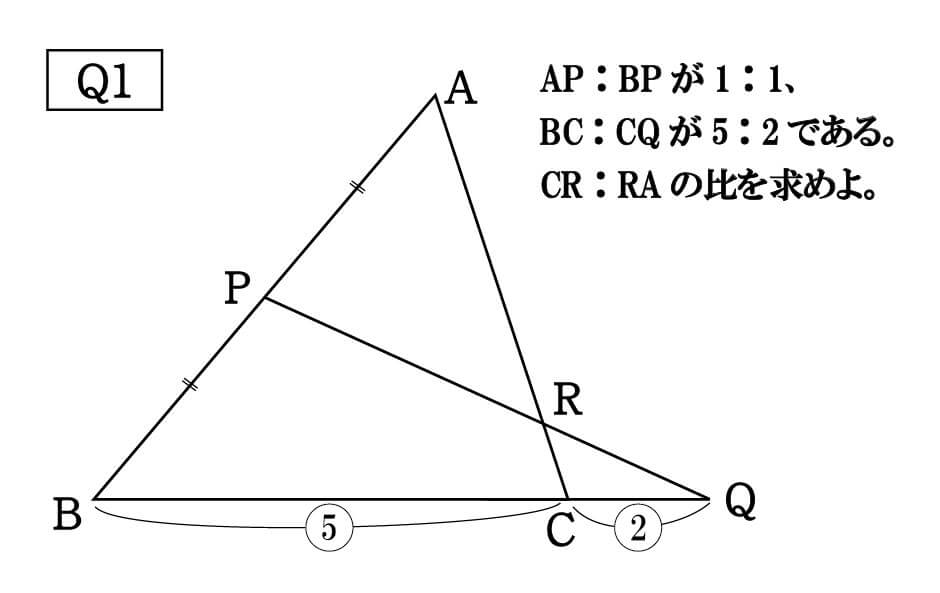
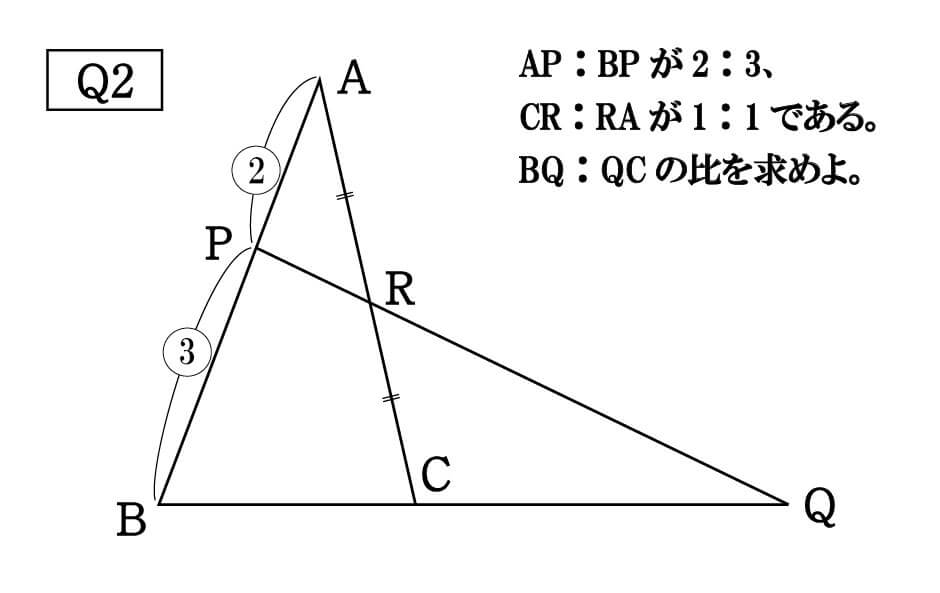
答えは以下の通りです。

これらの問題を、補助線を使うやり方で解こうとすると、2分では足りないでしょう。一方メネラウスの定理であれば、トレーニングを積むことで15秒あれば解けるようになります。

前回の記事 ⇒ 三角錐の体積比を楽に求められる公式
次の記事 ⇒ 正三角形の高さと面積は5秒で出せる!