切頭三角柱の体積を求める公式

前回に引き続き、斜めに切断された立体（切頭〇〇柱）の体積を求めるテクニックを紹介します。

今回は切頭三角柱です。早速例題を見てみましょう。

 

 

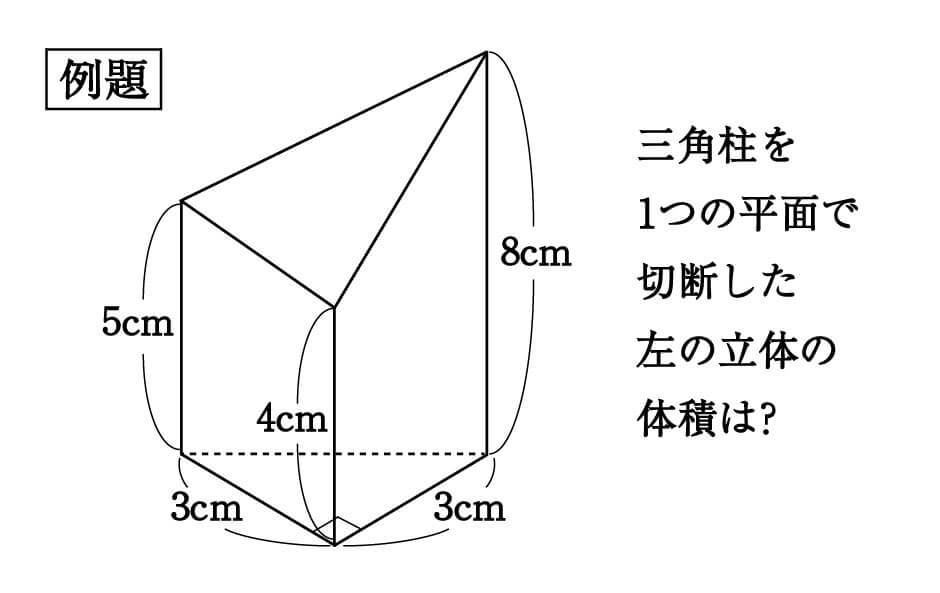
この問題を普通に解こうとすると、かなり手間がかかります。

しかし、切頭三角柱の場合も、前回と同じく［底面×高さの平均］という考え方が当てはまり、そのまま公式として使えるのです。

 

 

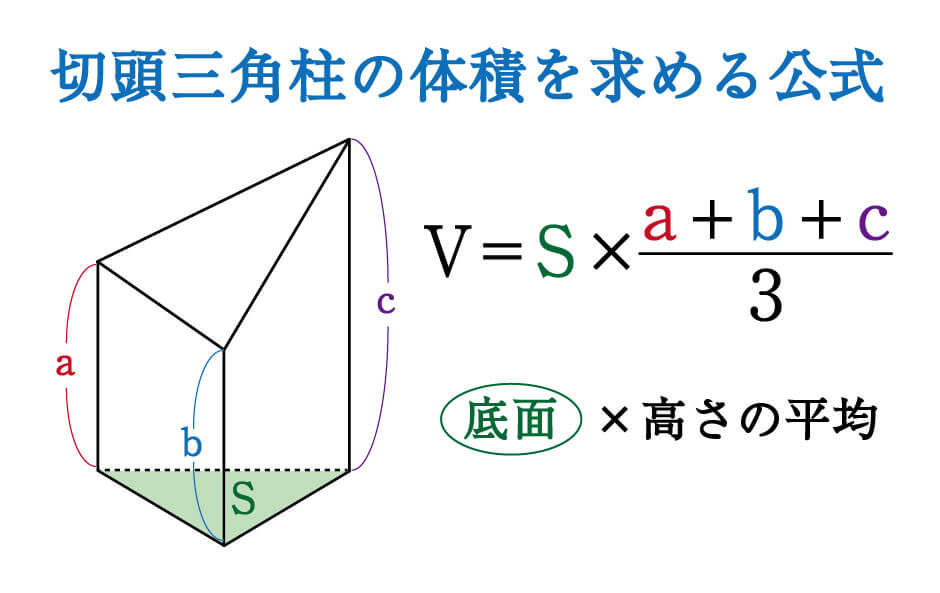
この公式を例題に当てはめると、次のようになります。
\begin{eqnarray}\frac{3×3}{2}×\frac{5+4+8}{3} = \frac{51}{2}cm^3 \\
\end{eqnarray}

 

切頭円柱の場合は、同じ立体を重ねて半分にするという発想で公式を証明することができましたが、三角柱の場合は一筋縄ではいきません。よって、ここでは証明を省略します。

 

 

さて、切頭三角柱の問題にはいくつかヴァリエーションがあり、中には次のような問題も登場します。

 

 

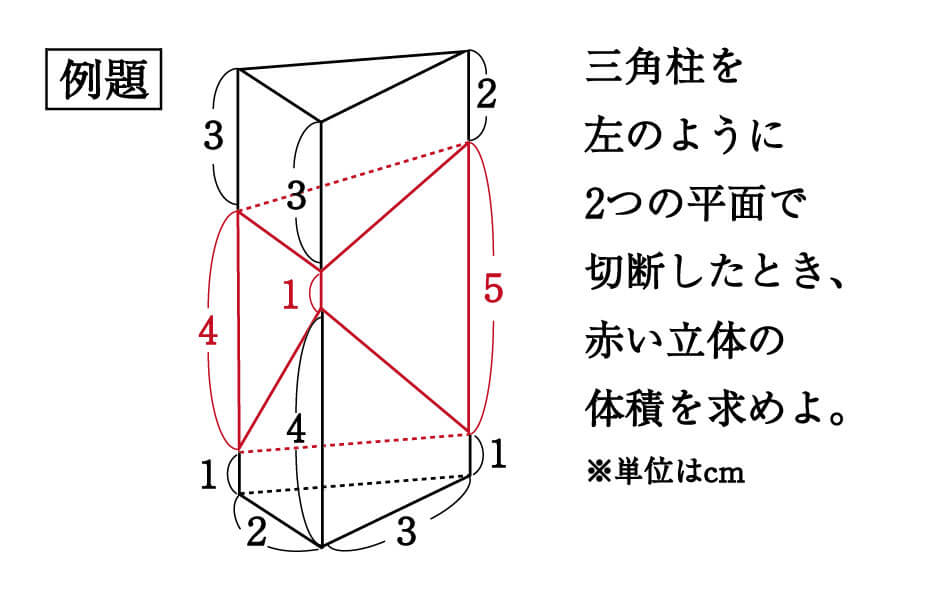
高さ\(8cm\)の三角柱があり、2ヵ所で斜めに切断されています。

それによってできた3つの異なる立体のうち、真ん中の赤い立体の体積はいくつか？という問題です。

 

先ほどの公式を理解できていれば、上と下の切頭三角柱の体積を求め、全体の体積から引けば答えが出せますよね。

この考え方でもそれほど多くの時間をかけずに解答できますが、実は今から教える方法であれば秒殺することが可能です。

 

その計算がこちら。

 

\begin{eqnarray}\frac{2×3}{2}×\frac{4+1+5}{3} = 10cm^3 \\
\end{eqnarray}

 

底面積に赤い立体を囲っている3辺の長さの平均をかければ、答えが出てしまうんです。

驚きではないですか？

 

なぜこの計算で解けるのかというと、実は切頭三角柱の公式は、底面から浮いている立体でも、3辺が底面に対して垂直な線であれば成り立つのです。

 

 

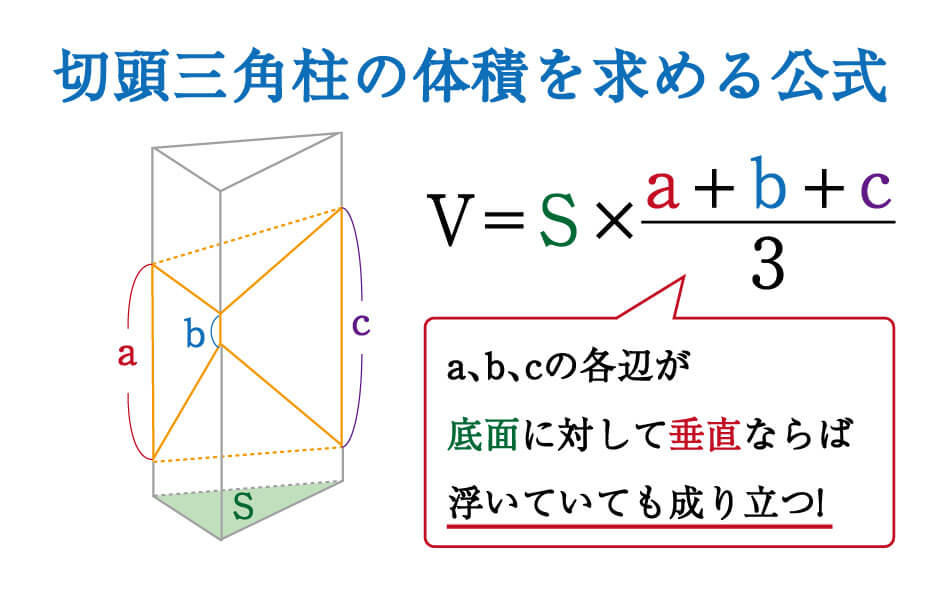
別の問題を使って、トレーニングしてみましょう。

 

 

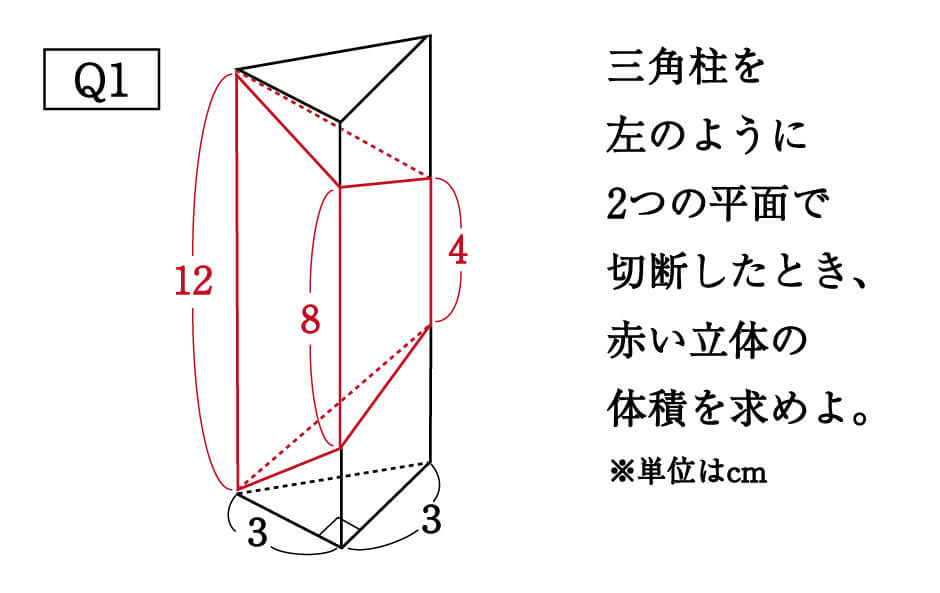
以下が答えです。

やはり公式を使うことで、ほとんど手間をかけることなく答えを出すことができます。

 

\begin{eqnarray}\frac{3×3}{2}×\frac{12+8+4}{3} = 36cm^3 \\
\end{eqnarray}

 

前回の記事 ⇒ 斜めに切断された円柱/四角柱の体積は、こう解くべし!
次の記事 ⇒ 角の二等分線にまつわる絶対に覚えておきたい公式