17種類の‟型”で構成された面積比MAP

苦手な生徒が多い「面積比」の問題。

その解法のポイントを、全6回にわけて解説していきます。

 

前回の記事 ⇒ なぜ面積比の問題は苦手になるのか? 
第2回では、面積比の問題を解くために必要な図形の“型”を整理していきます。

 

前回解説した通り、頭の中で“型”がしっかり整理されていないと、問題を解こうとした時にどうしたら良いかわからない、どう攻めたら良いかわからない、ということになってしまいます。

 

この“型”のまとめ方は人によって考え方が異なりますが、本記事では17種類にわけた‟面積比MAP”を紹介しておきましょう。

 

【面積比MAP】面積比問題を解くための17種類の型

↑クリックするとPDFが開きます。

 

★★★　…　Sランク：最重要の型。

★★　　…　Aランク：かなり重要な型。

★　　　…　Bランク：重要な型。

 

このように、知識というのはバラバラにインプットするのではなく、関連するものをまとめて同じ引き出しに入れ、整理しておくことが重要です。

そうすれば、本番で即座に必要な知識を引き出すことができます。

 

これら17つの型の中でも、★マークをつけたものはいずれも重要なのですが、本連載では受験生必修の6つのパターンに絞って解説していきます。

以下で紹介する2つの型は特に大事なので、しっかり学習していきましょう。

最重要! 絶対に押さえるべき2つのパターン

 

2つの三角形が背中合わせに、横に並んでいるパターンです。

この場合、どちらの三角形も高さは同じ。

ということは、2つの三角形の面積比は、底辺の比率と同じであるといえますよね。

 

高さが共通の隣り合う三角形の面積比は底辺比に等しい。

これが最重要の型のひとつです。

 

 

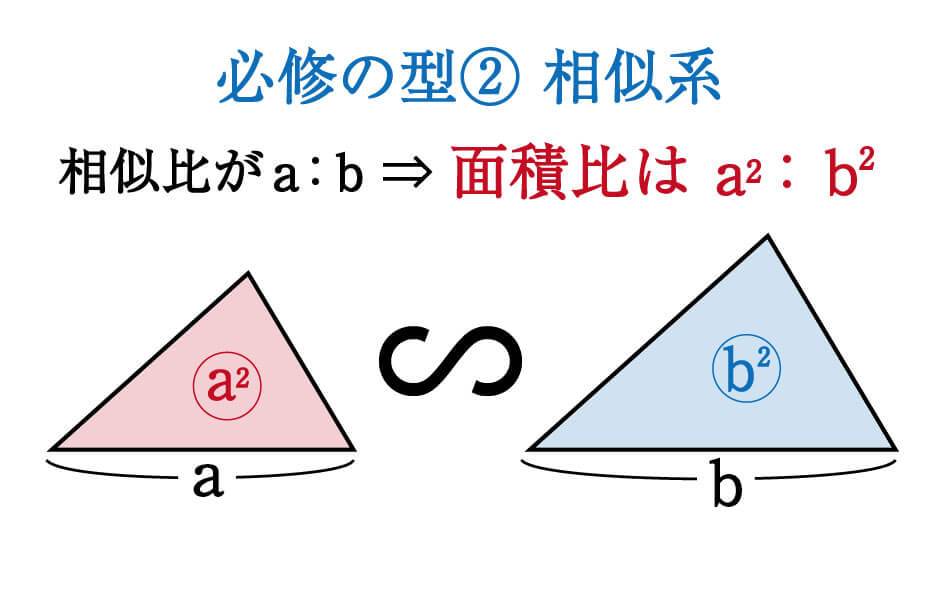
相似な関係にある2つの平面図形の相似比がa：bの場合、面積比はa²：b²になるという性質があります。

これがおぼえるべき、2つ目の型です。

 

さきほど示した17種類の内、14個は①と②をベースにしたものです。

よって、①②はもっとも基本となるパターンであり、すべての土台といえます。

 

ここで1つ例題を解いてみましょう。

 

 

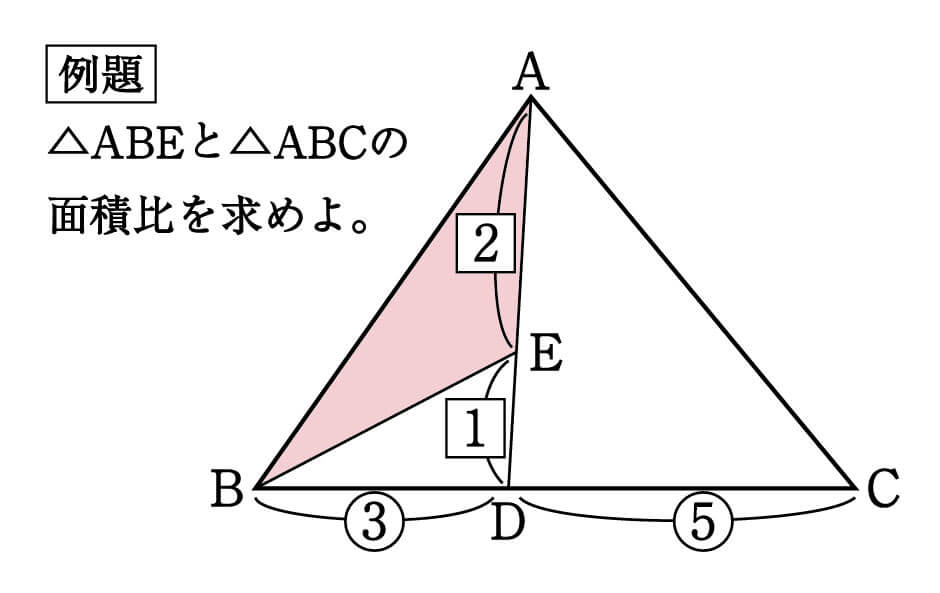
△ABCがあります。

辺BCを3：5にわける点をD、ADを2：1にわける点をEとしましょう。

この時、△ABEと△ABCの面積比を求めなさい、という問題です。

 

この場合、いきなり△ABEと△ABCを比べるのではなく、図形の中にある型を見抜けるかがポイント。

 

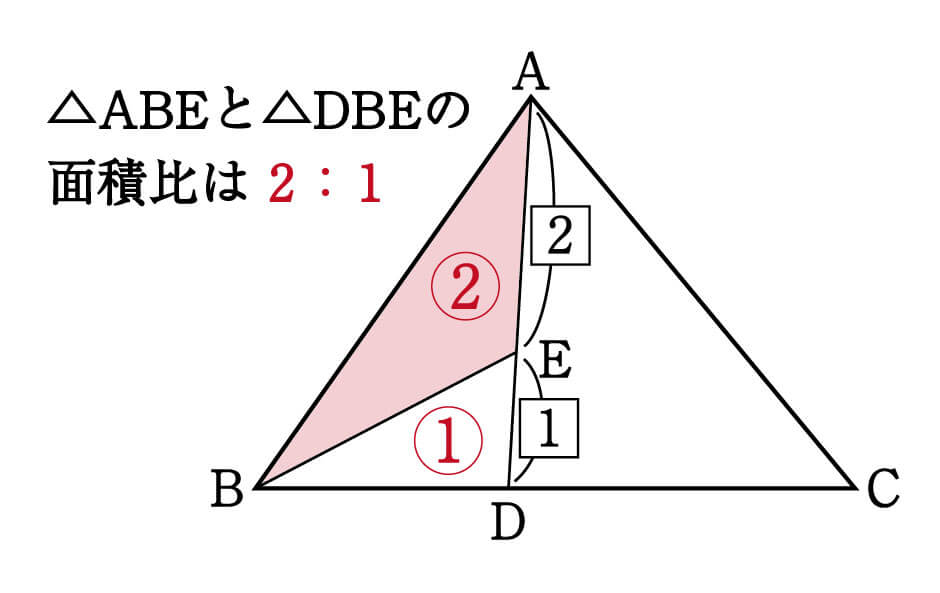
三角形の左側に注目すると、△ABEと△BDEは「高さが同じ隣り合う三角形」であることがわかります。

①の型に該当するので、2つの面積比は底辺比に等しい。つまり △ABE：△BDE＝2：1となるわけです。

 

 

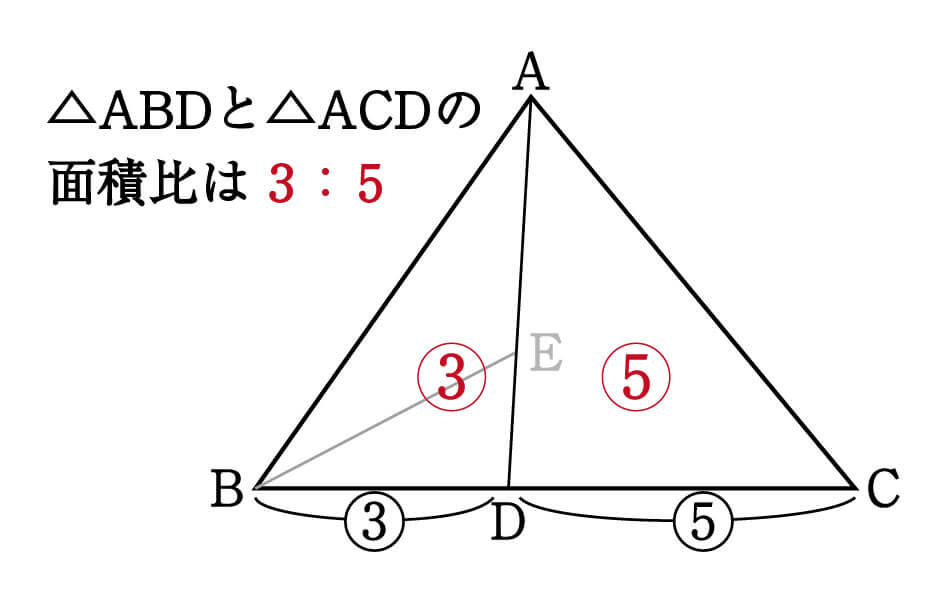
続いて、△ABDと△ACDを見てみると、こちらも①の型に当てはまります。

△ABDの面積を、△ABEと△BDEを合わせて3とした場合、△ABDと△ACDの面積比は、底辺の比が3：5なので、同じく3：5です。

 

 

△ABCの面積は3＋5＝8と表すことができるので、△ABE：△ABC＝2：8＝1：4。

このように、①の型を2回使うことで、正解にたどり着くことができました。

 

これは最も基本的な面積比の問題です。

次回から、より難しい問題に挑戦していきましょう。

 

次の記事 ⇒ 台形を4分割した図形パターン