基本的な解き方とより簡単に答えを出すための公式

苦手な生徒が多い「面積比」の問題。

その解法のポイントを、全6回にわけて解説していきます。

 

前回の記事 ⇒ 最重要パターン‟高さ共通”と”相似”

 

早速、例題を見てみましょう。

 

 

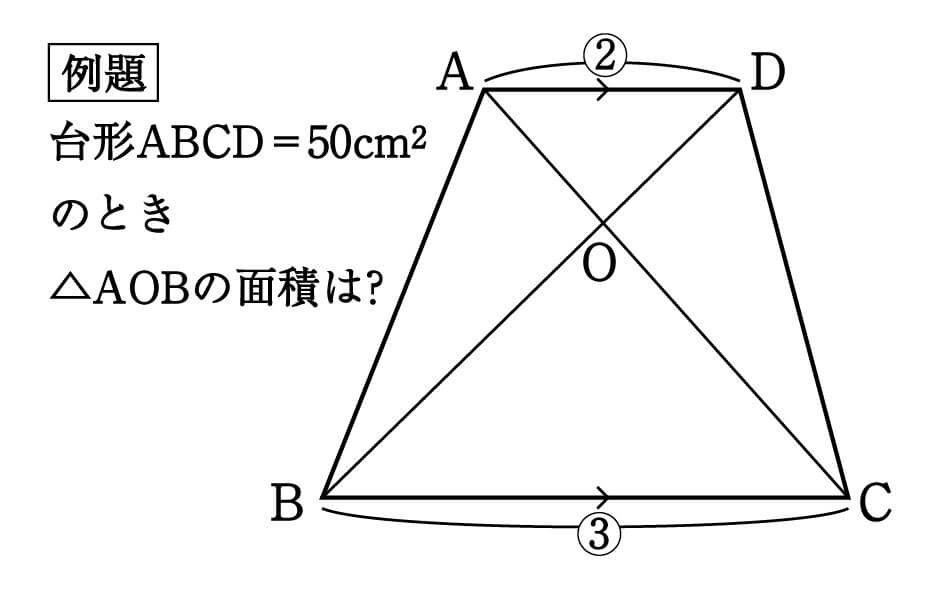
台形ABCDがあり、上底ADと下底BCの比は2：3です。

台形の面積が50cm²であるとき、△AOBの面積はいくつでしょうか？という問題です。

 

問題文には‟面積比”という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。

 

今回、最後に紹介する公式を使えば、簡単に答えを求めることもできますが、まずは前回学習した以下2つの型を使って解いてみましょう。

 

 

最初に注目すべきは、△ADOと△BCOが相似の関係であることです。

これに気がつけば、②の型を用いて面積比を求めることができます。

底辺の比が2：3なので面積比は、\(△ADO：△BCO＝2^2：3^2＝4：9\)となります。

 

 

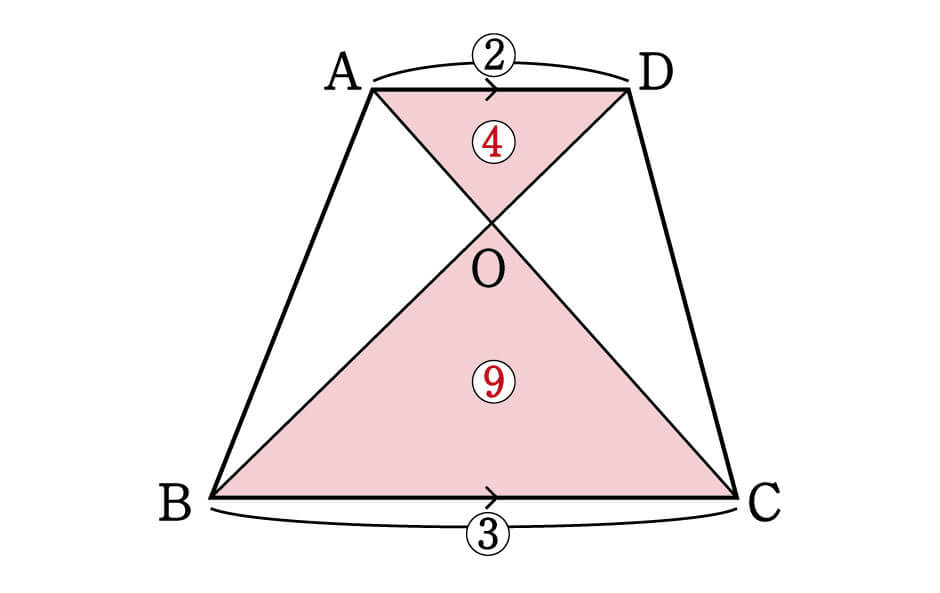
4：9というのはあくまで△ADOと△BCOの比の関係の数値であり、実際の面積ではありません。誤解しないよう気をつけてください。

 

続いて着目したいのが、△ADOと△ABO。

ここには、2つの三角形が背中合わせの状態になっている①の型が当てはまります。

 

ただし、底辺DOとBOの比率は書かれていません。

ここで、△ADOと△BCOが相似であることに再度注目してください。

ADとBCの比率が2：3であるのなら、相似の関係であるため、DO：BOも\(2：3\)ということができます。

 

 

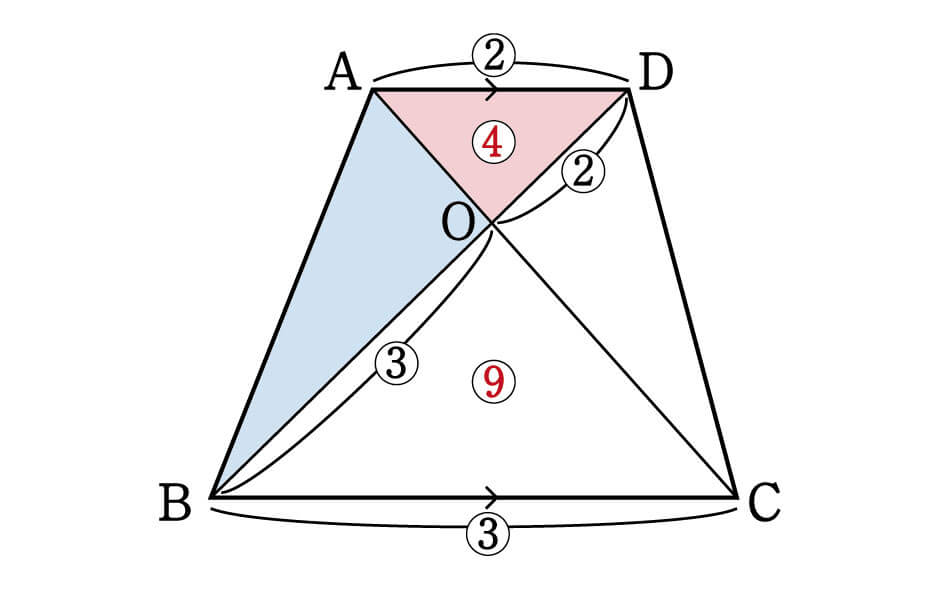
①の型である△ADOと△ABOの底辺比が2：3なので、面積比も2：3。

ただし、先ほど求めた△ADO：△BCO＝4：9という比の関係を維持しなくてはいけないので、\(△ADO：△ABO＝4：6\)としておきましょう。

 

△ADOと△DCOの面積比も、同じ理由で4：6になります。

 

 

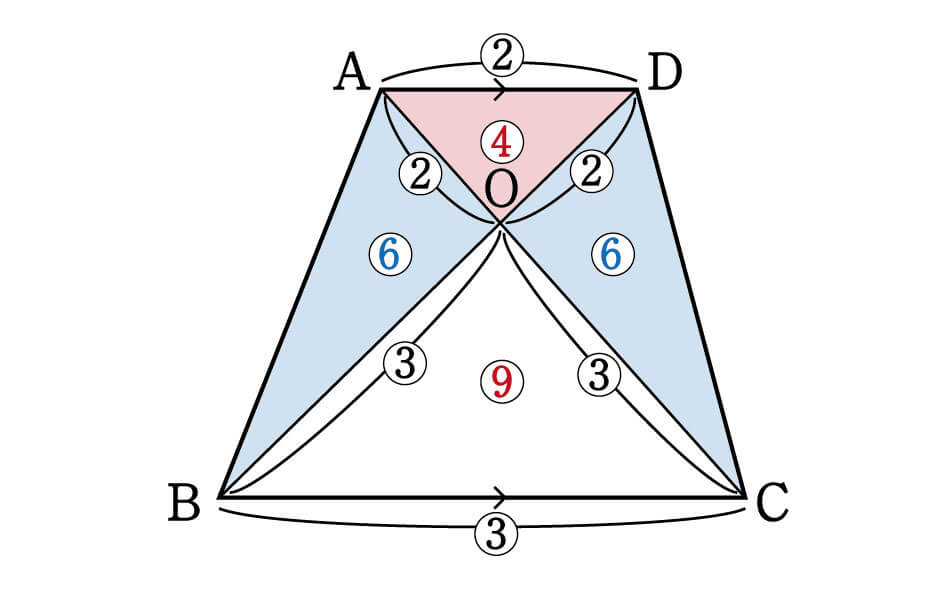
ここまでくれば、問われている△AOBの面積は、台形ABCDを25等分（4＋6＋6＋9）したうちの6つ分である、ということがわかります。

よって、以下の計算で△AOBの面積を求めましょう。

\begin{eqnarray}S=50×\frac{6}{25}＝2×6＝12\end{eqnarray}

 

答えは\(12cm^2\)です。

 

このように、①と②の型を使って問題を解くことができましたが、台形を4分割した図形の面積比を問う問題は頻出します。

そのため、以下の公式をおぼえてしまうのが良いでしょう。

 

 

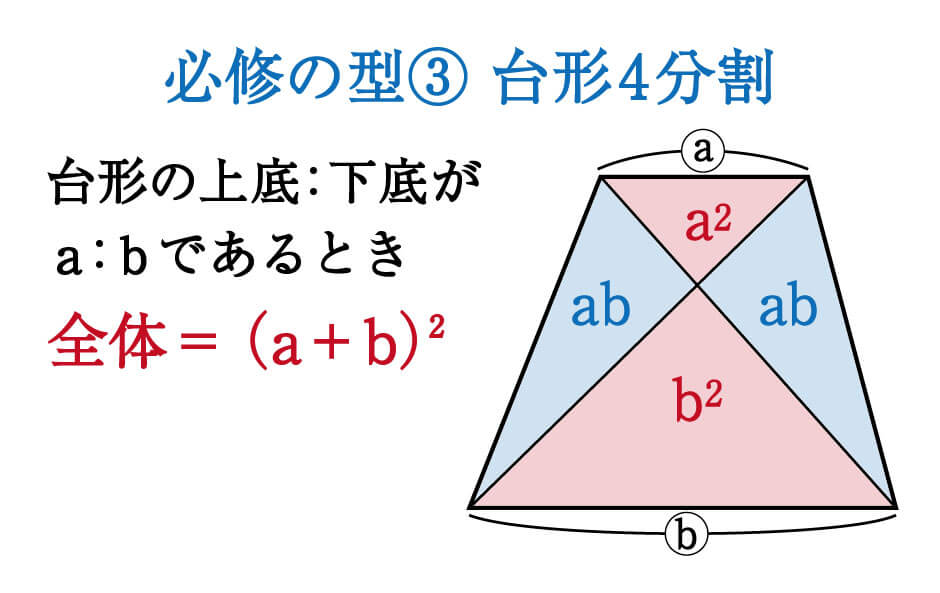
台形の上底：下底が\(a：b\)ならば、上下の三角形の面積比は\(a^2：b^2\)となり、左右の三角形の面積比は\(ab：ab\)である、という公式です。

また、全体は\(a^2＋b^2＋ab＋ab＝a^2＋2ab＋ b^2\)と表すことができ、さらに因数分解することで\(（a＋b）^2\)となります。

 

とても応用が利く型なので、①②の型と併せて必ずおぼえておきましょう。

 

次の記事 ⇒ 比の合成を極めよう!