異なる比を‟合成”して‟連比”を作り出す

苦手な生徒が多い「面積比」の問題。

その解法のポイントを、全6回にわけて解説していきます。

 

前回の記事 ⇒ 台形を4分割した図形パターン

 

面積比の問題を解く手順は合っていたけれど、比の扱いに慣れておらず正解が出せなかった……。

そういった残念なケースもあると思います。

 

面積比の問題で得点するためには、比を上手く扱えるようになることが重要です。

 

今回は、“比の合成”というテクニックを練習します。

必ず役に立つ手法なので、しっかり習得しましょう。

 

まずは、純粋な比の問題から見てみましょう。

 

 

これは小学校6年生の問題です。

 

母と弟を比べれば良いので、

\begin{eqnarray}母：弟&＝&9：11\\
162：x&＝&9：11 \\
x&＝&198cm
\end{eqnarray}

と計算してしまった方がいたら、これはまちがい。不正解です。

 

何がいけなかったのかというと、母と兄、兄と弟の身長比はそれぞれ別の関係であるにもかかわらず、そのまま母と弟をつなげてしまったことが、大きなミスでした。

 

① 母：兄　　 ＝ 9：8

② 　　兄：弟 ＝ 　 12：11

 

このように2つの比を並べてみると、兄の身長比の数字が異なっているとわかります。

よって、兄の数字を揃えなければ、母と弟を比較することはできません。

 

そのため、兄の身長比を8と12の最小公倍数である24にしてみましょう。

それに合わせて、母の身長比を3倍、弟の身長比を2倍します。

 

① 母：兄　　 ＝ 9：8

② 　　兄：弟 ＝ 　 12：11

↓ ①を3倍、②を2倍

① 母：兄　　 ＝ 27：24

② 　　兄：弟 ＝ 　     24：22

 

これをまとめると、次のように表せます。

 

母：兄：弟 ＝ \(27：24：22\)

 

このように、3つ以上の項目を並べた比率を「連比」といいます。

2つの異なる比を「合成」して、「連比」を作ったわけです。

 

この連比を使えば、母と弟を比較して正解を導き出せます。

\begin{eqnarray}母：弟&=&27：22\\
162：x&＝&27：22\\
x&=&\frac{162×22}{27} \\
\\
x&＝&132cm
\end{eqnarray}
続いて、比の合成を面積比の問題に適用してみましょう。

 

 

△ABCがあり、辺BCを3：5にわける点がD、ADを4：3にわける点がEとなっています。

このとき、△ABEの面積は△ABCの何倍でしょうか？

 

解き方は前回と同じです。

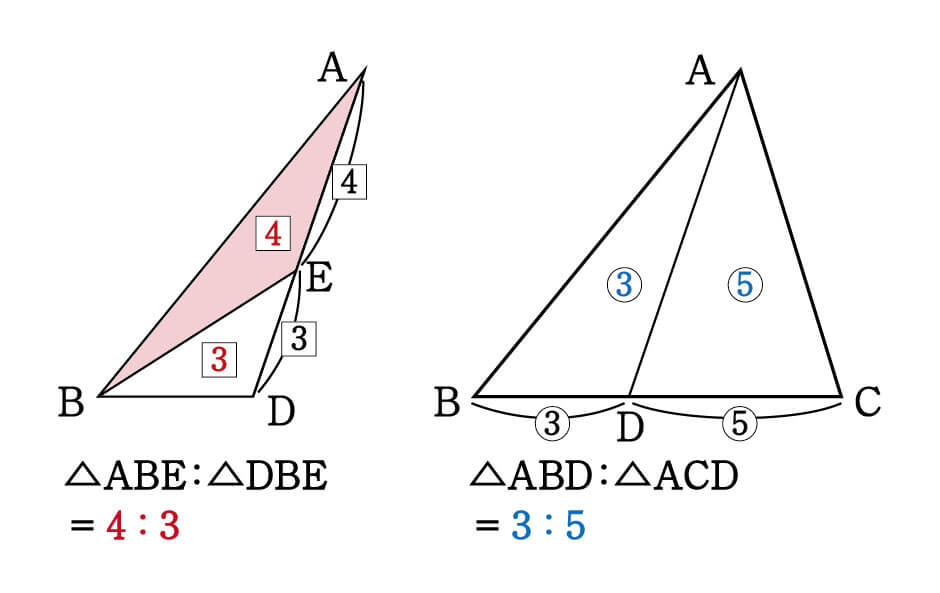
まず△ABEの隣に、背中合わせで並んだ高さが同じ△BDEがあります。

底辺の比がAE：DE＝4：3なので、面積比も\(△ABE：△BDE＝4：3\)。

また、△ABDと△ACDも①の型になっているので、底辺の比＝3：5より、面積比は\(△ABD：△ACD＝3：5\)となります。

 

 

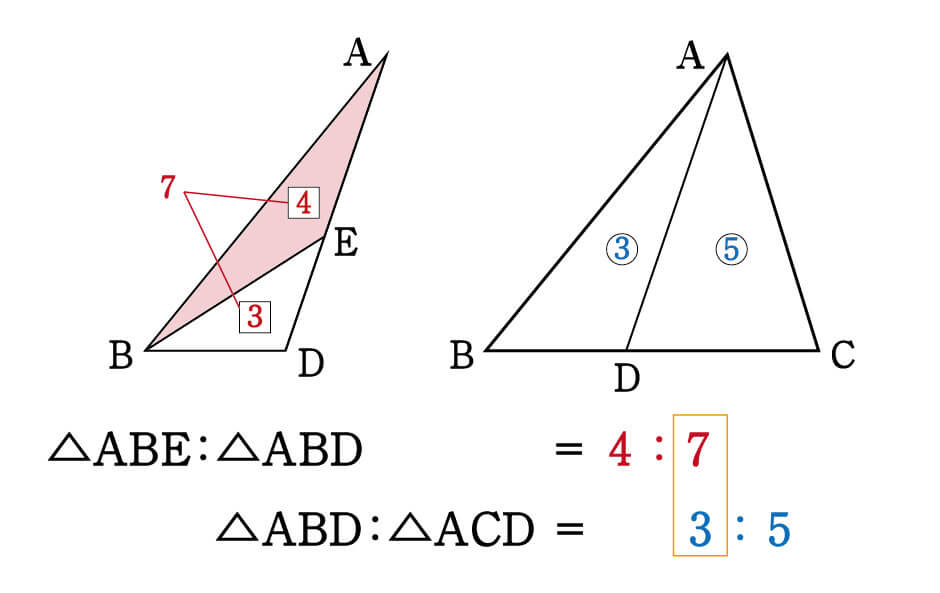
ここからが重要です。

いま作った2つの比を使って答えを出したいのですが、以下のように△ABDの数字が合いません。

 

 

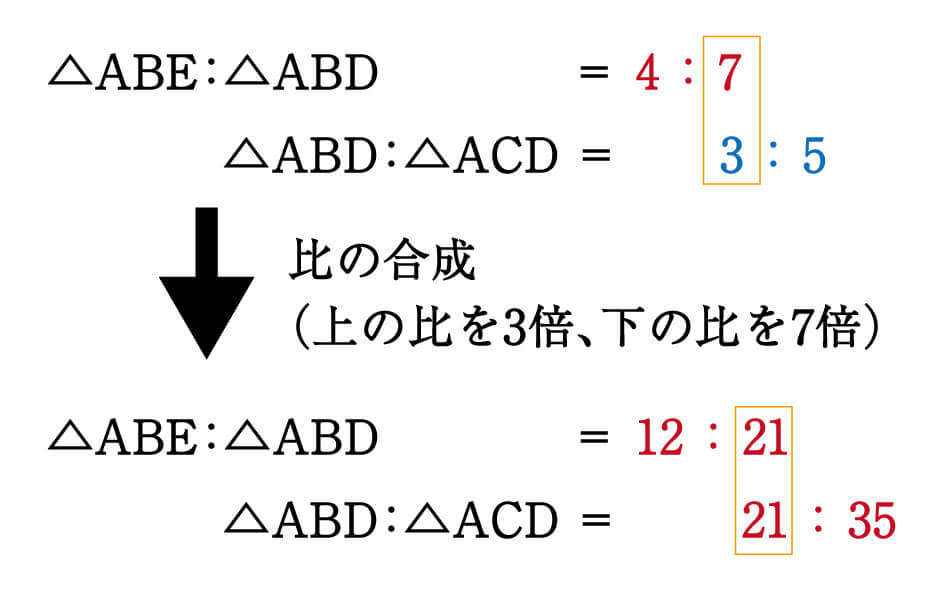
ここで、比の合成を使います。

7と3を、最小公倍数の21に揃えましょう。

 

 

これを図に表してみます。

 

 

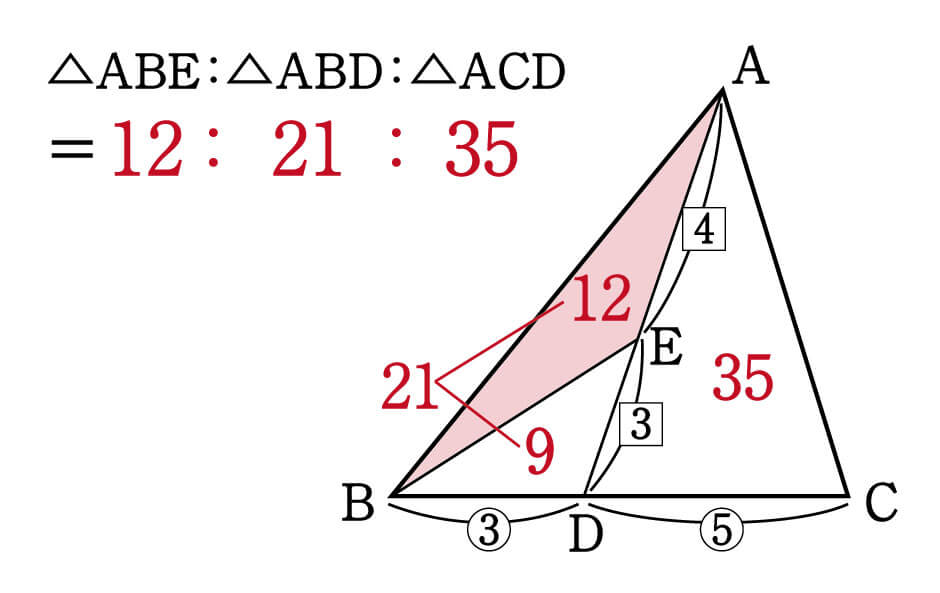
\(△ABE\)は\(12\)、全体は\(12＋9＋35＝56\)となるので、答えは\(12÷56＝\cfrac{3}{14}倍\)です。

 

次の記事 ⇒ 面積比は全体から攻めると求めやすい!?