全体の面積がどのように分割されているのか考える

苦手な生徒が多い「面積比」の問題。

その解法のポイントを、全6回にわけて解説していきます。

 

前回までの面積比問題の解き方は、イメージとしては内側の分割された図形から分析し、全体に迫っていくという流れでした。

 

つまり部分から全体に向かって攻めていたわけですが、今回学ぶアプローチは真逆です。

全体の面積がどのように分割されているのか、という発想で解いていきます。

 

実はこちらの方が、考えやすい問題が多いです。

ただし、前回までのやり方であれば整数で計算できたのに対し、今回のアプローチでは分数が必ず登場します。

 

第4回と同じ例題で説明しましょう。

 

 

 

△ABCがあり、辺BCを3：5にわける点がD、ADを4：3にわける点がEとなっています。

このとき、△ABEの面積は△ABCの何倍でしょうか？

 

まず、△ABCの面積をSとしておきましょう。

その上で、2つのステップを踏んで解いていきます。

 

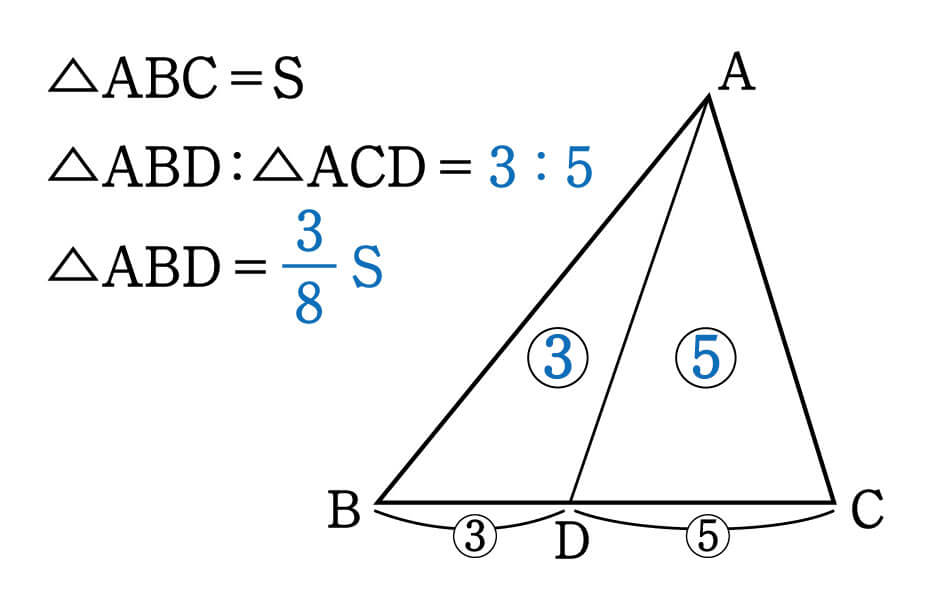
1つ目のステップでは、△ABDと△ACDの面積比に注目します。

隣り合う三角形の①の型なので、底辺の比＝3：5から面積比も3：5。

そして左側の△ABDは、△ABCを8等分したうちの3つ分ですから、\(△ABD\)の面積＝\(\displaystyle \frac{3}{8}S\)と表すことができます。

 

 

次に、△ABEと△ABDの面積比を考えましょう。

こちらも①の型であり、底辺比が4：3なので△ABE：△DBE＝4：3です。

つまり△ABEの面積は、△ABDを7等分したうちの4つ分と考えることができます。

 

 

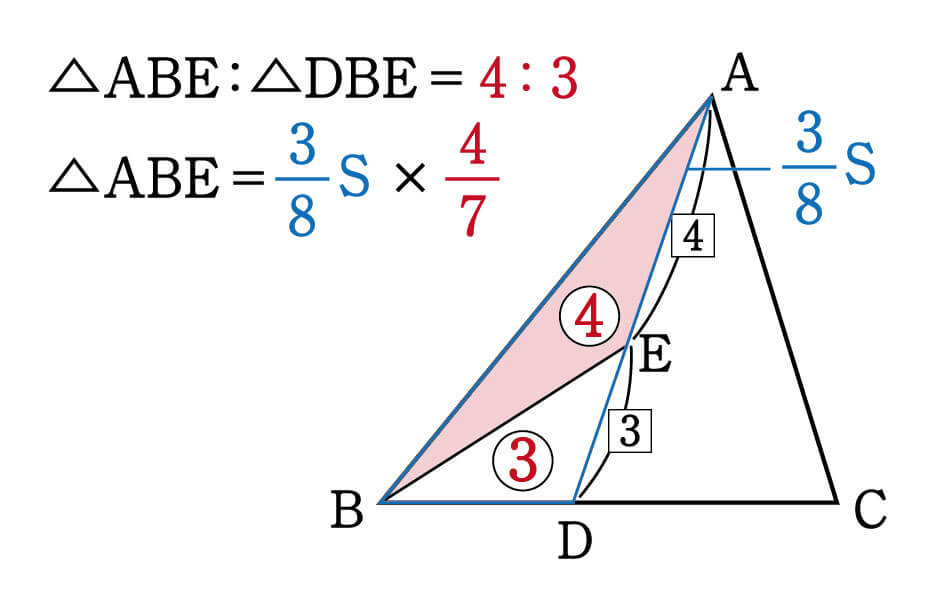
よって、△ABEの面積は以下の式で求めることができますね。

\begin{eqnarray}△ABE＝\frac{3}{8}S×\frac{4}{7}＝\frac{3}{14}S\end{eqnarray}

△ABEの面積は△ABCの何倍か？という問いに対する答えは、\(\displaystyle \cfrac{3}{14}\)倍です。

 

このように、全体から攻めていくことで、比の合成を使うよりも比較的簡単に解くことができます。

 

この手法を使って、もう1問解いてみましょう。

第1回で、はじめに紹介した問題です。

 

 

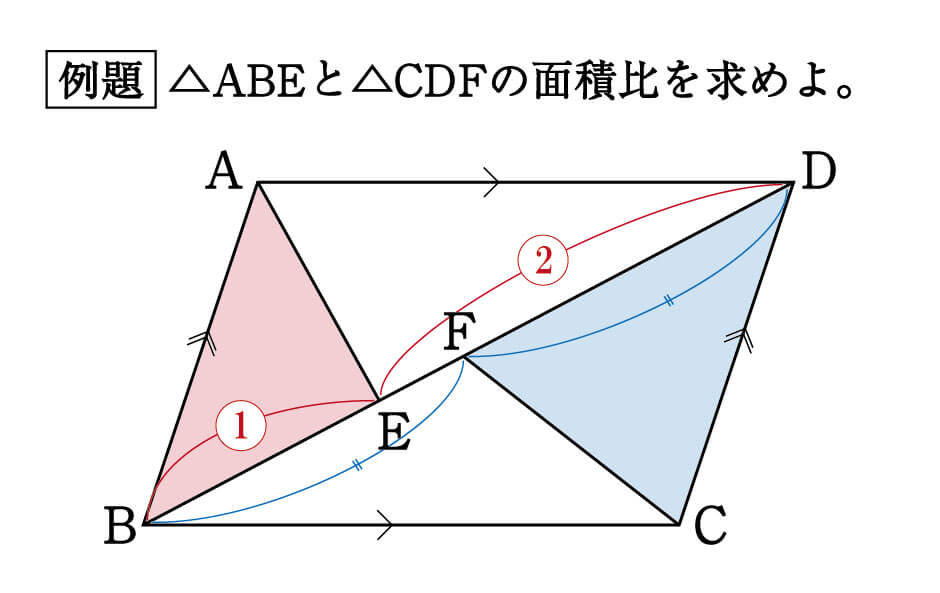
平行四辺形ABCDがあり、対角線BDを1：2にわける点がE、BDの中点がFとなっています。

このとき、△ABEと△CDFの面積比を求めなさい。

 

この問題を解く上で、4つ目の型をおぼえてもらいたいと思います。

 

 

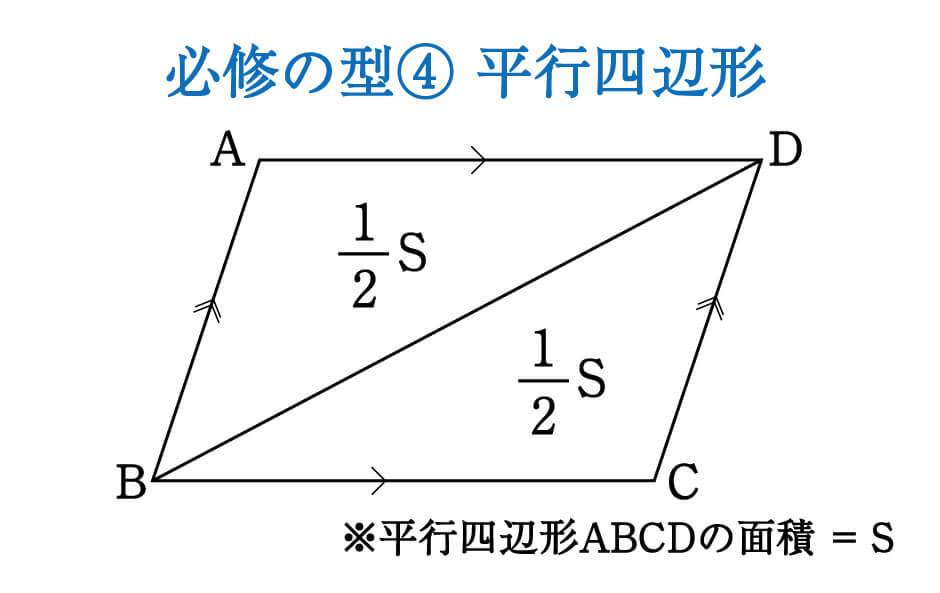
平行四辺形は対角線を1本引くと2等分されます。

対角線BDによってABCDはちょうど半分になっているので、△ABDと△BCDの面積はそれぞれ\(\displaystyle \frac{1}{2}S\)です。

 

続いて△ABDを見てみましょう。

△ABEと△ADEの面積比は、底辺比と同じなので1：2。

つまり、△ABEは△ABDを3等分したうちの1つ分なので、以下のように表せます。

 

\(△ABE\)の面積\(＝\displaystyle \frac{1}{2}S×\frac{1}{3}＝\frac{1}{6}S\)

 

一方、△BCFと△DCFを見てみると、FはBDの中点なので、それぞれの面積は△BCDを二等分したものとわかります。

 

\(△DCF\)の面積\(＝\displaystyle \frac{1}{2}S×\frac{1}{2}＝\frac{1}{4}S\)

 

 

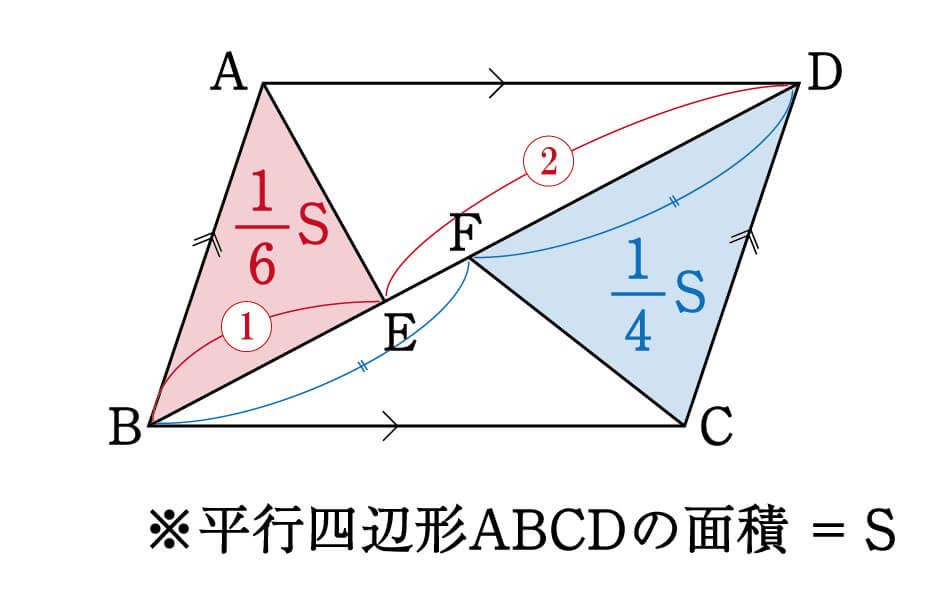
これで、△ABEと△DCFの面積を、全体に対する割合で表すことができました。

あとは比を作り、計算するだけです。

 

\begin{eqnarray}\frac{1}{6}S：\frac{1}{4}S＝2：3\end{eqnarray}

 

今回の新しいアプローチであれば、図形内にある離れた2つの三角形の面積比でも簡単に答えることが可能です。

 

次の記事 ⇒ “対角線の入った台形” “一角共有の三角形”