台形を対角線でわけたときにできる三角形の面積比

苦手な生徒が多い「面積比」の問題。

その解法のポイントを、全6回にわけて解説していきます。

 

前回の記事 ⇒ 面積比は全体から攻めると求めやすい!?

 

これまでの内容が身についていれば、基本的な面積比の問題は解けるようになっているはずです。

最後のレッスンでは、新しい“型”を2つおぼえていきましょう。

 

 

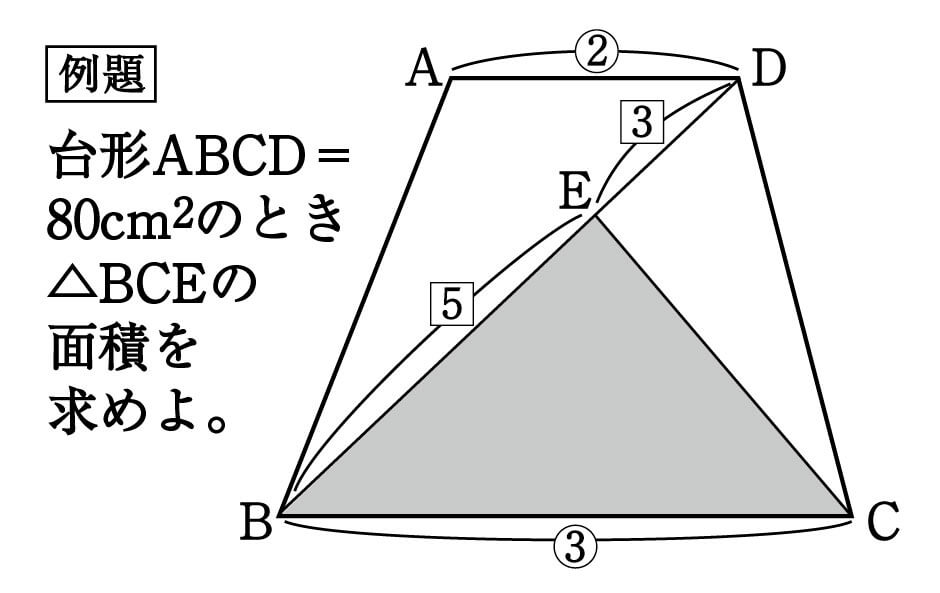
台形ABCDがあり、上底：下底は2：3、対角線BDを5：3にわける点がEとなっています。

台形ABCDの面積が80cm²のとき、△BCEの面積はいくつでしょうか。

 

まずは、この問題を解くための、新しい型を紹介します。

 

 

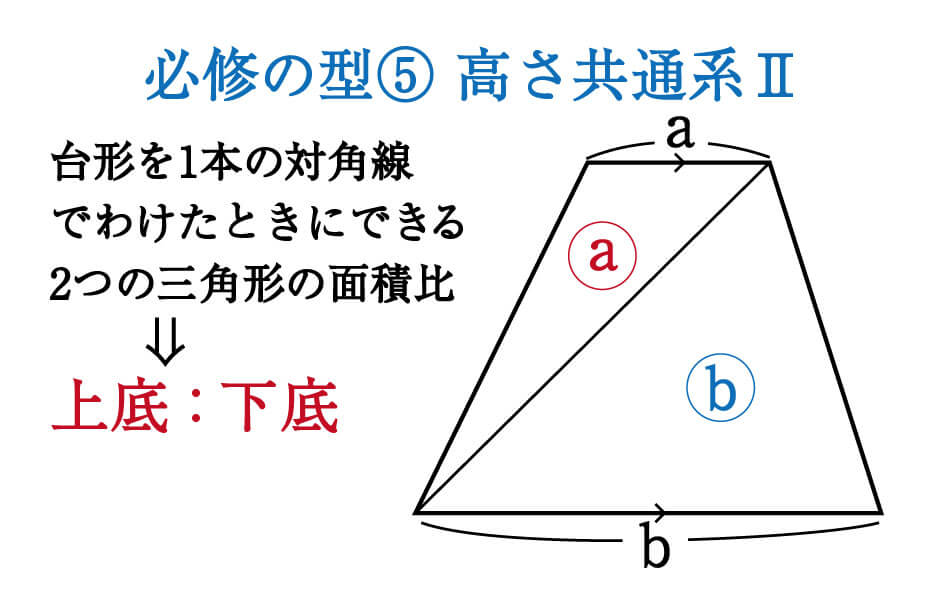
こちらは全く新しい知識というわけではなく、高さが同じ2つの三角形が隣り合っている①の型の仲間といえます。

台形を1本の対角線でわけたときにできる2つの三角形は、上底と下底が平行であるため、高さが共通です。そのため、面積比は上底と下底の比と等しくなるのです。

 

この⑤の型を踏まえて、例題を解いてみましょう。

 

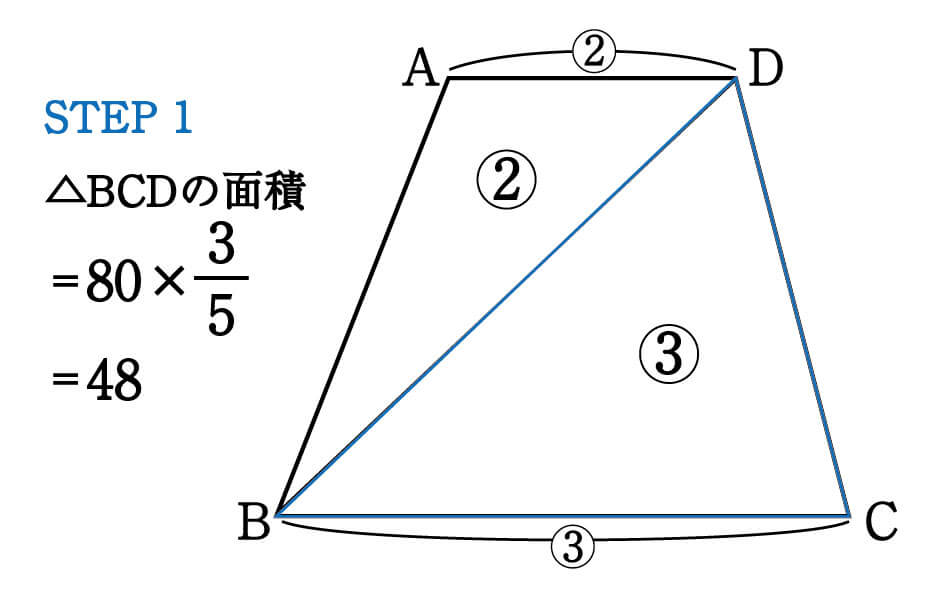
例題の台形ABCDは対角線BDで2つの三角形にわけられます。

よって、△ABDと△BCDの面積比は上底（AD）と下底（BC）の比と等しいので2：3。

△BCDは台形全体を5等分したうちの3つ分なので、その面積は以下となります。

 

\begin{eqnarray}△BCD＝80×\frac{3}{5}＝48cm^2\end{eqnarray}

 

 

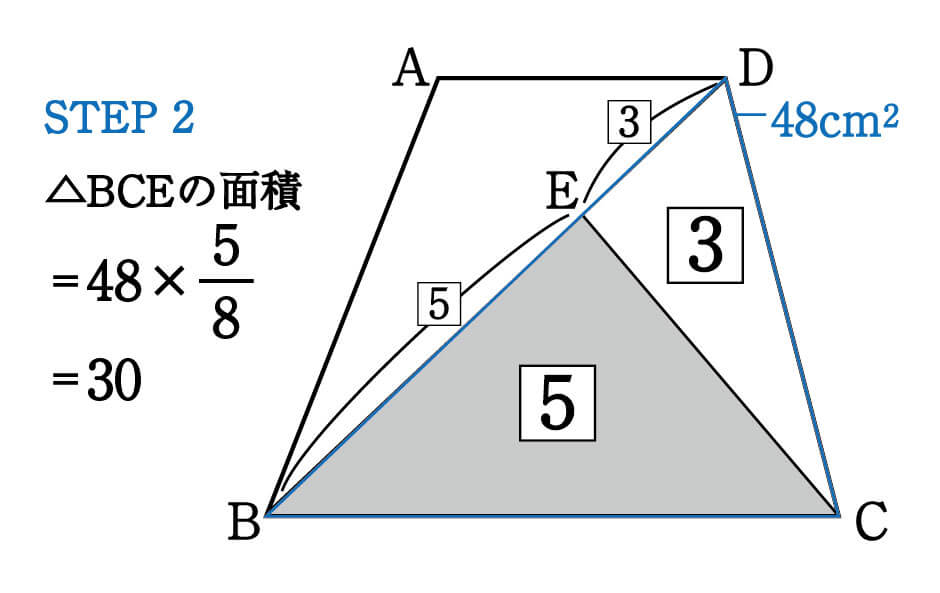
続いて、△BCEと△CDEが隣り合う三角形の型であることに注目。

底辺の比が5：3なので、両者の面積比も5：3です。

つまり、△BCEは△BCDを8等分したうちの5つ分だとわかります。

こちらが答えです。

 

\begin{eqnarray}△BCE＝48×\frac{5}{8}＝30cm^2\end{eqnarray}

 

ひとつの角を共有する2つの三角形の面積比

 

 

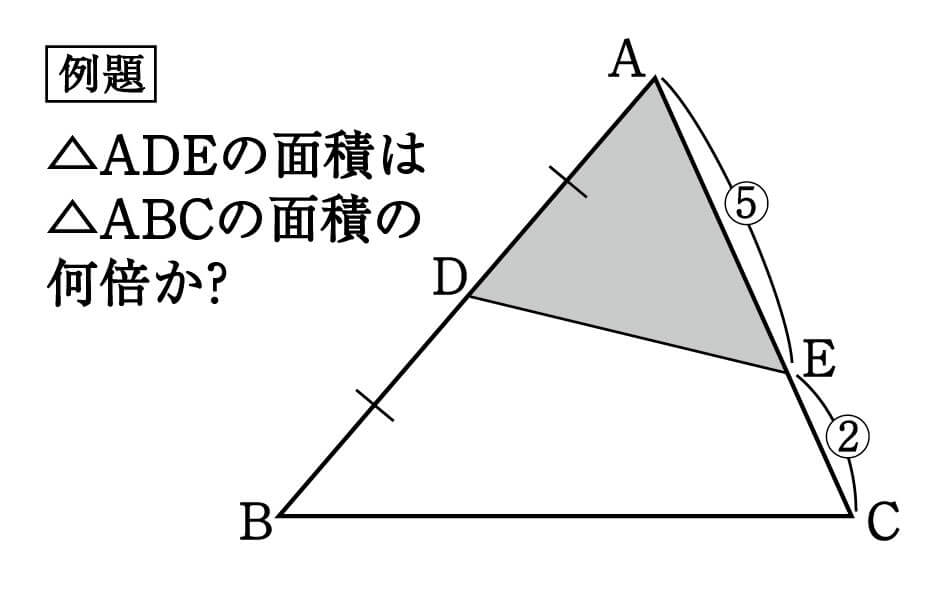
△ABCがあり、ABの中点がD、ACを5：2にわける点がEとなっています。

このとき、△ADEの面積は△ABCの何倍でしょうか？

 

これをそのまま解こうとすると、今まで習ったいずれの型も当てはまらないので、次に進めません。

そこで、補助線を引きましょう。

 

 

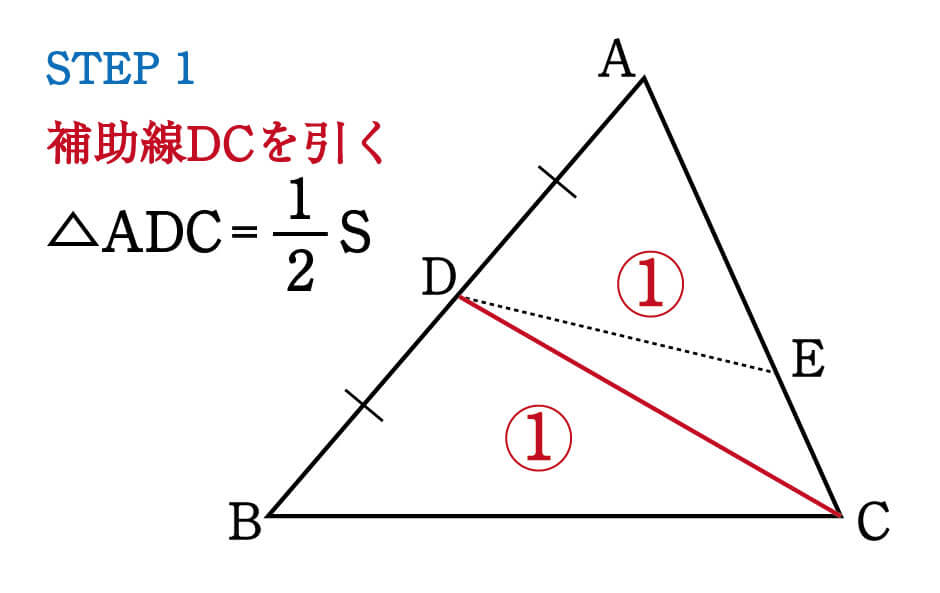
今回は、隣り合わせの三角形の型①を作るために、DCという補助線を引きました。

そうすると、全体の面積をSとしたとき、点DはABの中点なので、△ADCの面積を\(\displaystyle \frac{1}{2}S\)と表すことができます。

 

 

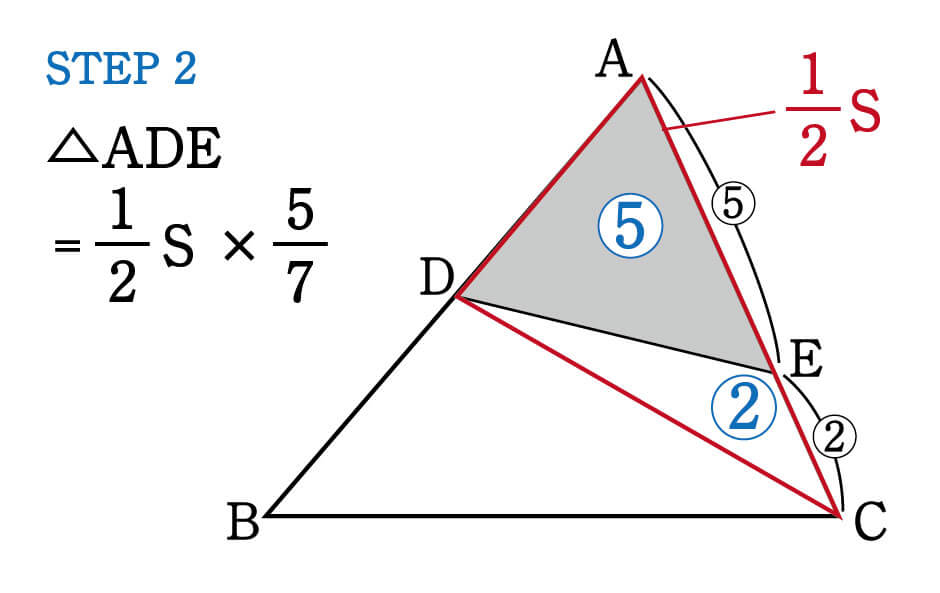
続いて、△ADCの中を見てみると、△ADEと△CDEが①の型になっているので、底辺の比5：2と同じく、\(△ADE：△CDE\)も\(5：2\)。

つまり、△ADEは△ADC（\( \frac{1}{2}S\)）を7等分したうちの5つ分なので、その面積は次の通りです。

 

\begin{eqnarray}△ADE＝\frac{1}{2}S×\frac{5}{7} = \frac{5}{14}S \end{eqnarray}

 

例題の答えは、\(\displaystyle \frac{5}{14}\)倍となります。

 

このように、補助線を1本引くことでスムーズに解くことができましたが、「ひとつの角を共有する2つの三角形」という一角共有のパターンは非常によく登場します。

そのため、次の公式をおぼえてしまいましょう。

 

 

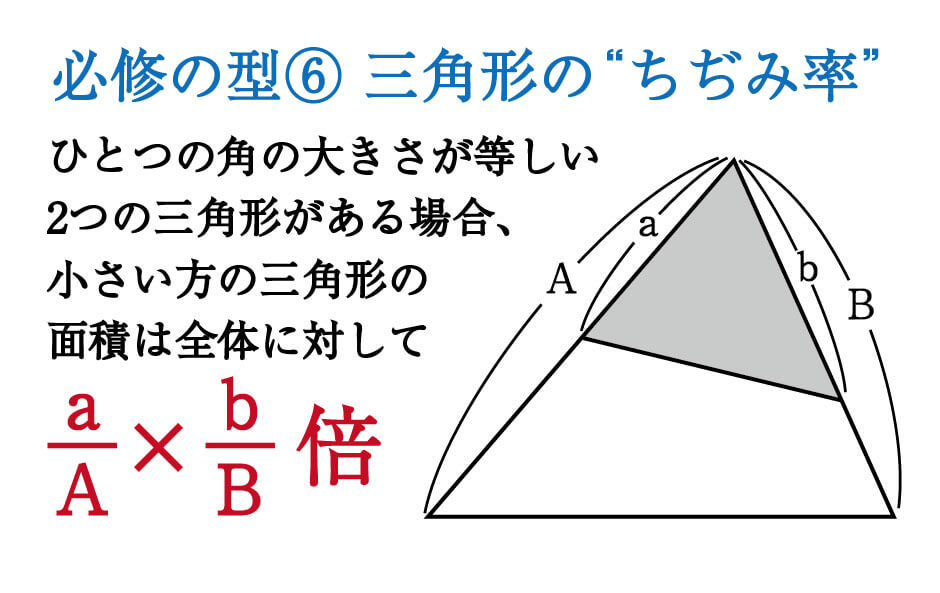
なお、“ちぢみ率”というのはこのレッスンだけで使用している言葉で、決して一般的な名称ではないので注意してください。

 

これにて「“面積比”集中特訓」は終了です。